(人教版)2023-2024学年九年级数学上册 23.1 图形的旋转 期中专项复习
试卷更新日期:2023-10-11 类型:复习试卷
一、选择题
-
1. 如图,把绕点顺时针旋转某个角度得到 , 则旋转角等于( )
 A、 B、 C、 D、2. 菱形ABCD的边长为2,∠A=60°,将该菱形绕顶点A在平面内旋转30°,则旋转后的图形与原图形重叠部分的面积为( )A、3- B、2- C、-1 D、2-23. 如图,将△ABC绕点C顺时针旋转,点B的对应点为点E , 点A的对应点为点D,当点E恰好落在边AC上时,连接AD , 若∠ACB=30°,则∠DAC的度数是( )
A、 B、 C、 D、2. 菱形ABCD的边长为2,∠A=60°,将该菱形绕顶点A在平面内旋转30°,则旋转后的图形与原图形重叠部分的面积为( )A、3- B、2- C、-1 D、2-23. 如图,将△ABC绕点C顺时针旋转,点B的对应点为点E , 点A的对应点为点D,当点E恰好落在边AC上时,连接AD , 若∠ACB=30°,则∠DAC的度数是( ) A、60° B、65° C、70° D、75°4. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( )
A、60° B、65° C、70° D、75°4. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( ) A、 B、 C、 D、5. 如图,将绕点A顺时针旋转得到 , 若线段 , 则的长为( )
A、 B、 C、 D、5. 如图,将绕点A顺时针旋转得到 , 若线段 , 则的长为( ) A、3 B、4 C、5 D、66. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( )
A、3 B、4 C、5 D、66. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( ) A、4 B、4 C、4 D、47. 如图所示,将一个含角的直角三角板绕点逆时针旋转,点的对应点是点 , 若点、、在同一条直线上,则三角板旋转的度数是( )
A、4 B、4 C、4 D、47. 如图所示,将一个含角的直角三角板绕点逆时针旋转,点的对应点是点 , 若点、、在同一条直线上,则三角板旋转的度数是( ) A、 B、 C、 D、8. 如图1,△ABC和△ADE都是等腰直角三角形,∠D和∠ACB都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( )
A、 B、 C、 D、8. 如图1,△ABC和△ADE都是等腰直角三角形,∠D和∠ACB都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( ) A、45°,90° B、90°,45° C、60°,30° D、30°,60°9. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( )
A、45°,90° B、90°,45° C、60°,30° D、30°,60°9. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB//x轴,交y轴于点P.将△OAP绕点O 顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB//x轴,交y轴于点P.将△OAP绕点O 顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A的坐标为( ) A、( , -1) B、(-1,) C、( , -1) D、(1,)
A、( , -1) B、(-1,) C、( , -1) D、(1,)二、填空题
-
11. 如图,在中, , 把绕点逆时针旋转得到 , 连结CD,则CD的长为.
 12. 如图,将△ABC绕着点顺时针旋转到△ADE的位置,使点首次落在上.已知 , , 则 .
12. 如图,将△ABC绕着点顺时针旋转到△ADE的位置,使点首次落在上.已知 , , 则 . 13. 如图,点E在正方形的边上,将绕点A顺时针旋转90°到的位置,连接 , 过点A作的垂线,垂足为点H,与交于点G,若 , , 则的长为 .
13. 如图,点E在正方形的边上,将绕点A顺时针旋转90°到的位置,连接 , 过点A作的垂线,垂足为点H,与交于点G,若 , , 则的长为 .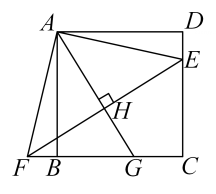 14. 如图所示,直线与x轴,y轴分别交于A,B两点,把绕点A旋转后得到 , 则点的坐标是 .
14. 如图所示,直线与x轴,y轴分别交于A,B两点,把绕点A旋转后得到 , 则点的坐标是 .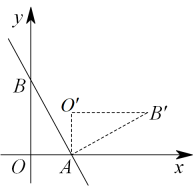 15. 如图,在中, , , , 将绕点A顺时针旋转得到 , 使点在的延长线上,则的长为.
15. 如图,在中, , , , 将绕点A顺时针旋转得到 , 使点在的延长线上,则的长为.
三、解答题
-
16. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
 17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.
17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.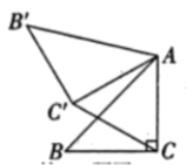 18. 如图,将矩形绕点C顺时针旋转得到矩形 , 点B与点E对应,点E恰好落在边上,交于点H,求证:.
18. 如图,将矩形绕点C顺时针旋转得到矩形 , 点B与点E对应,点E恰好落在边上,交于点H,求证:. 19. 如图,在中, , 将绕点C逆时针旋转50°得到 , 且于点D,求的度数.
19. 如图,在中, , 将绕点C逆时针旋转50°得到 , 且于点D,求的度数.
四、综合题
-
20. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上.
 (1)、求证:AE平分;(2)、连接BD,求证: .21. 在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)、求证:AE平分;(2)、连接BD,求证: .21. 在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E. (1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
(1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.