(人教版)2023-2024学年九年级数学上册 22.2 二次函数与一元二次方程 期中专项复习
试卷更新日期:2023-10-11 类型:复习试卷
一、选择题
-
1. 设 , 下表列出了与的6对对应值:
根据表格能够发现一元二次方程的一个解的大致范围是( )
A、 B、 C、 D、2. 已知、是一元二次方程的两个不相等的实数根,、是一元二次方程的两个不相等的实数根,其中若 , 则的值为( )A、 B、 C、 D、3. 如图,抛物线与轴交于点 , 顶点坐标为 , 与轴的交点在、之间不包含端点 , 则的取值范围是( ) A、 B、 C、 D、4. 如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 , 则小朱本次投掷实心球的成绩为( )
A、 B、 C、 D、4. 如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 , 则小朱本次投掷实心球的成绩为( ) A、7m B、7.5m C、8m D、8.5m5. 若二次函数的图象经过点 , 则方程的解为( )A、 B、 C、 D、6. 已知 , 关于x的一元二次方程的解为 , 则下列结论正确的是( )A、 B、 C、 D、7. 如图所示的是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A、7m B、7.5m C、8m D、8.5m5. 若二次函数的图象经过点 , 则方程的解为( )A、 B、 C、 D、6. 已知 , 关于x的一元二次方程的解为 , 则下列结论正确的是( )A、 B、 C、 D、7. 如图所示的是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )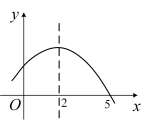 A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>58. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个9. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,10. 由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>58. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个9. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,10. 由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )x
1.0
1.1
1.2
1.3
x2+12x
13
14.41
15.84
17.29
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、14.41<x<15.84二、填空题
-
11. 二次函数是常数,的自变量与函数值的部分对应值如下表:
当时,与其对应的函数值有下列结论:;和是关于的方程的两个根;则所有正确结论的序号为 .
12. 已知二次函数 的图象如图所示,则一元二次方程的解是 .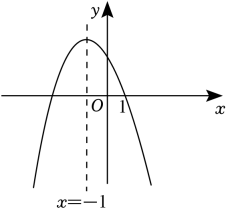 13. 抛物线如图所示,利用图象可得方程的近似解为(精确到0.1).
13. 抛物线如图所示,利用图象可得方程的近似解为(精确到0.1).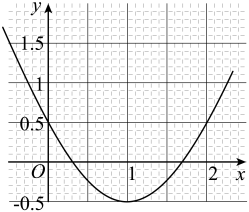 14. 二次函数的部分图象如图所示,则方程的根为 .
14. 二次函数的部分图象如图所示,则方程的根为 .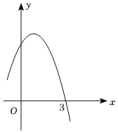 15. 抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
15. 抛物线上部分点的横坐标x,纵坐标y的对应值如下表:…
-3
-2
0
1
3
5
…
…
7
0
-8
-9
-5
7
…
则方程的解是.
三、解答题
-
16. 已知点为二次函数图像上的点,求代数式的值.17. 若二次函数的对称轴为直线 , 求关于x的方程的解.18. 已知二次函数 试证明:不论m取何值,这个二次函数的图象必与x轴有两个交点19. 由数形结合思想知:解方程可以看成是求两个函数交点的横坐标。例如:解方程2x+3=-x-6可看成是求直线y=2x+3和直线y=-x-6的交点横坐标。利用这一思想方法,借助函数图象,判断方程: 的实数根有几个。
四、综合题
-
20. 如图,抛物线经过 , 两点,与x轴交于另一点B,连接 , .
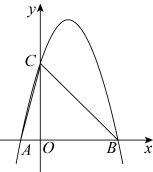 (1)、求抛物线的解析式;(2)、平行于x轴的直线与抛物线分别交于点D,E,求线段的长.21. 已知关于的方程 .(1)、若该方程的一个根为1,求的值及该方程的另一根;(2)、求证:二次函数的图象与轴有两个交点.22. 已知二次函数 .
(1)、求抛物线的解析式;(2)、平行于x轴的直线与抛物线分别交于点D,E,求线段的长.21. 已知关于的方程 .(1)、若该方程的一个根为1,求的值及该方程的另一根;(2)、求证:二次函数的图象与轴有两个交点.22. 已知二次函数 .…
-4
-3
-2
-1
0
1
2
…
…
-6
-1
____
3
2
____
-6
…
 (1)、填写表,并在给出的平面直角坐标系中画出这个二次函数的图象;(2)、根据表格结合函数图象,直接写出方程的近似解(指出在哪两个连续整数之间即可).23. 如图,在平面直角坐标系中,已知抛物线的顶点为 , 与轴交于点 , 线段轴,交该抛物线于另一点 .
(1)、填写表,并在给出的平面直角坐标系中画出这个二次函数的图象;(2)、根据表格结合函数图象,直接写出方程的近似解(指出在哪两个连续整数之间即可).23. 如图,在平面直角坐标系中,已知抛物线的顶点为 , 与轴交于点 , 线段轴,交该抛物线于另一点 . (1)、求点的坐标及直线的解析式;(2)、当二次函数的自变量满足时,此函数的最大值为 , 最小值为 , 且 , 求的值;(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线只有一个公共点时,设此时抛物线的顶点的横坐标为 , 请直接写出的取值范围.
(1)、求点的坐标及直线的解析式;(2)、当二次函数的自变量满足时,此函数的最大值为 , 最小值为 , 且 , 求的值;(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线只有一个公共点时,设此时抛物线的顶点的横坐标为 , 请直接写出的取值范围.