（人教版）2023-2024学年九年级数学上册 21.3 实际问题与一元二次方程 期中专项复习

试卷更新日期：2023-10-11 类型：复习试卷

进入 出卷网 下载

一、选择题

  • 1. 要组织一次足球邀请赛，参赛的每两个队之间都要比赛一场.计划安排28场比赛，应邀请多少个队参赛（ ）
    A、6 B、7 C、8 D、9

    查看试题解析

  • 2. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ）
    A、12x(x+1)=4×7 B、12x(x−1)=4×7 C、x(x+1)=28 D、x(x−1)=28

    查看试题解析

  • 3. 要组织一次篮球联赛，赛制为单循环形式（每两队之间都只赛一场），计划安排15场比赛，如果设邀请x个球队参加比赛，那么根据题意可以列方程为（   ）
    A、2x=15 B、x(x+1)=15 C、x(x−1)=15 D、x(x−1)2=15

    查看试题解析

  • 4. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批椽，这批椽的价钱为6210文.如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是（    ）
    A、3(x−1)x=6210 B、3(x−1)=6210 C、(3x−1)x=6210 D、3x=6210

    查看试题解析

  • 5. 有若干个好朋友除夕夜晚打电话互相问候，两个朋友之间都通话交流一次，一共通话21次，设这些朋友一共x人，则下列方程正确的是（    ）
    A、12x(x+1)=21 B、x(x+1)=21 C、12x(x−1)=21 D、x(x−1)=21

    查看试题解析

  • 6. 一次足球联赛实行单循环比赛（每两支球队之间都比赛一场），计划安排15场比赛，设应邀请了x支球队参加联赛，则下列方程中符合题意的是（    ）
    A、12x(x+1)=15 B、12x(x−1)=15 C、x(x+1)=15 D、x(x−1)=15

    查看试题解析

  • 7. 在一次同学聚会上，大家一见面就相互握手（每两人只握一次）．大家共握了21次手．设参加这次聚会的同学共有x人，根据题意，可列方程为（    ）
    A、x(x+1)=21 B、12x(x+1)=21 C、x(x−1)=21 D、12x(x−1)=21

    查看试题解析

  • 8. 若两个连续奇数的积为63，则这两个数的和为（    ）
    A、16 B、17 C、±16 D、±17

    查看试题解析

  • 9. 有一个两位数，个位数字与十位数字之和为8，把它的个位数字与十位数字对调，得到一个新数，新数与原数之积为1855，则原两位数是（   ）
    A、35 B、53 C、62 D、35或53

    查看试题解析

  • 10. “绿水青山就是金山银山”，某地为打造绿色产业，实行退耕还林，若计划2022年退耕还林10万公顷，以后退耕还林面积逐年递减，递减率均为10%，那么预计2024年退耕还林的面积为（    ）
    A、10万公顷 B、9万公顷 C、8.1万公顷 D、7.29万公顷

    查看试题解析

二、填空题

  • 11. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了28条航线，则这个航空公司共有个飞机场.．

    查看试题解析

  • 12. 方程x2-6x+8＝0的两个根是等腰三角形的底和腰，则这个等腰三角形周长是 ．

    查看试题解析

  • 13. 某种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支，主干、支干和小分支的总数是91，那么每个支干长出小分支.

    查看试题解析

  • 14. 在2020年太原五中秋季运动会上，某班参加圆周接力的同学每两人握一次手，共握手190次，设参加圆周接力的人数为x，则可列方程为.

    查看试题解析

  • 15. 一个两位数，个位数字比十位数字少1，且个位数字与十位数字的乘积等于72，则这个两位数是 ．

    查看试题解析

三、解答题

  • 16. 新冠病毒肆虐全球，我国的疫情很快得到了控制，并且研发出安全性、有效性均非常高的疫苗.经调查发现，北京生物制药厂有1条生产线，最大产能是42万支/天，若每增加1条生产线，每条生产线的最大产能将减少2万支/天，现该厂要保证每天生产疫苗144万支，在既增加产能的同时又节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

    查看试题解析

  • 17. 某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是43，求这种植物每个支干长出的小分支个数

    查看试题解析

  • 18. 解读诗词(通过列方程算出周瑜去世时的年龄)：大江东去浪淘尽，千古风流数人物，而立之年督东吴，早逝英年两位数，十位恰小个位三，个位平方与寿符，哪位学子算得快，多少年华属周瑜？诗词大意：周瑜三十岁当东吴都督，去世时的年龄是两位数，十位数字比个位数字小三，个位数字的平方等于他去世时的年龄.

    查看试题解析

  • 19. 我们知道，传销能扰乱一个地方正常的经济秩序，是国家法律明令禁止的．某非法传销组织现有一名头目计划每人发展若干数目的下线，每个下线再发展同样数目的下线成员．经过两轮发展后，非法传销组织成员共有57人，间每个人计划发展下线多少人？

    查看试题解析

四、综合题

  • 20. 某校团体操表演队伍有6行8列，后又增加了51人，使得团体操表演队伍增加的行、列数相同，
    (1)、求增加了多少行或多少列？
    (2)、若团体操表演队在某次文艺汇演，租表演服装每套要50元，化妆每人10元，需支付经费多少元？

    查看试题解析

  • 21. 如图，Rt△ABC中，∠C=90° ， BC=a ， AC=b(a<b) ， AB=5 ， a ， b是方程x2−(m−1)x+(m+4)=0的两根.

    (1)、求a ， b；
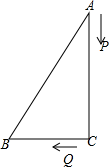    (2)、P ， Q两点分别从A ， C出发，分别以每秒2个单位，1个单位的速度沿边AC ， BC向终点C ， B运动，（有一个点达到终点则停止运动），求经过多长时间后PQ=2？

    查看试题解析

  • 22. 某市为鼓励居民节约用水，对居民用水实行阶梯收费，每户居民用水量每月不超过a吨时，每吨按0.3a元缴纳水费；每月超过a吨时，超过部分每吨按0.4a元缴纳水费．
    (1)、若a＝12，某户居民3月份用水量为22吨，则该用户应缴纳水费多少元？
    (2)、若如表是某户居民4月份和5月份的用水量和缴费情况：

    月份

    用水量（吨）

    交水费总金额（元）

    4

    18

    62

    5

    24

    86

    根据上表数据，求规定用水量a的值

    查看试题解析

  • 23. 应用题：（本题第一问要求列方程作答）

    某市要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排15场比赛．

    (1)、应该邀请多少支球队参加比赛？
    (2)、若某支球队参加3场后，因故不参与以后的比赛，问实际共比赛多少场？

    查看试题解析