(人教版)2023-2024学年八年级数学上册 13.4 课题学习 最短路径问题 期中专项复习
试卷更新日期:2023-10-11 类型:复习试卷
一、选择题
-
1. 小颖的爸爸要在某条街道l上修建一个奶站P,向居民区A,B提供牛奶,要使点P到A,B的距离之和最短,则下列作法正确的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
2. 如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( ) A、 B、 C、a+b D、a3. 如图,等边和等腰 , , 点E,F分别为边 , 的中点,若的面积为16, , 点M是CE上的动点,则的周长的最小值为( )
A、 B、 C、a+b D、a3. 如图,等边和等腰 , , 点E,F分别为边 , 的中点,若的面积为16, , 点M是CE上的动点,则的周长的最小值为( ) A、6 B、8 C、9 D、104. 如图,过边长为2的等边的顶点C作直线 , 然后作关于直线l对称的 , P为线段上一动点,连接 , , 则的最小值是( )
A、6 B、8 C、9 D、104. 如图,过边长为2的等边的顶点C作直线 , 然后作关于直线l对称的 , P为线段上一动点,连接 , , 则的最小值是( ) A、4 B、3 C、2 D、15. 如图,在中, , 平分 , 点E是的中点,点P是上一动点,连接 , 若 , , , 则的最小值是( )
A、4 B、3 C、2 D、15. 如图,在中, , 平分 , 点E是的中点,点P是上一动点,连接 , 若 , , , 则的最小值是( ) A、 B、6 C、 D、106. 如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若 , 当取得最小值时,则的度数为( )
A、 B、6 C、 D、106. 如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若 , 当取得最小值时,则的度数为( ) A、 B、 C、 D、7. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( )
A、 B、 C、 D、7. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( ) A、7 B、8 C、9 D、108. 如图,中, , 垂直平分 , 点P为直线上一动点,则的最小值为( )
A、7 B、8 C、9 D、108. 如图,中, , 垂直平分 , 点P为直线上一动点,则的最小值为( ) A、3 B、5 C、6 D、79. 如图,在中, , 、是的两条中线, , P是上一个动点,则的最小值是( )
A、3 B、5 C、6 D、79. 如图,在中, , 、是的两条中线, , P是上一个动点,则的最小值是( ) A、7 B、3.5 C、5 D、2.510. 如图,在中, , 是的垂直平分线,与交于点 , 与 交于点F,D为边的中点,M为线段上一个动点.若 , 的面积为16,则周长的最小值为( )
A、7 B、3.5 C、5 D、2.510. 如图,在中, , 是的垂直平分线,与交于点 , 与 交于点F,D为边的中点,M为线段上一个动点.若 , 的面积为16,则周长的最小值为( ) A、7 B、8 C、9 D、10
A、7 B、8 C、9 D、10二、填空题
-
11. 如图,在ςABC中,AB=AC,直线MN垂直平分AB,点D为BC的中点,点E为线段MN上一动点,若BC=4,等腰△ABC面积为12,则△BDE的周长的最小值为.
 12. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.
12. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.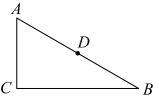 13. 如图,等腰的底边长为4,面积是16,腰的垂直平分线分别交 , 边于E,F点,若点D为边的中点,点M为线段上一动点,则周长的最小值为.
13. 如图,等腰的底边长为4,面积是16,腰的垂直平分线分别交 , 边于E,F点,若点D为边的中点,点M为线段上一动点,则周长的最小值为. 14. 如图所示,在边长为2的等边中,点为的中点,点为的中点,过点作交于点 , 交于点 , 点是线段上一个动点,连接 , , 则的周长的最小值是.
14. 如图所示,在边长为2的等边中,点为的中点,点为的中点,过点作交于点 , 交于点 , 点是线段上一个动点,连接 , , 则的周长的最小值是. 15. 如图,在中, , , , 直线l是边的垂直平分线,点P是直线l上的一动点,则的最小值为 .
15. 如图,在中, , , , 直线l是边的垂直平分线,点P是直线l上的一动点,则的最小值为 .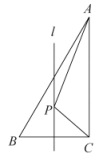
三、解答题
-
16. 某高速公路的同一侧有A,B两个城镇,如图所示,它们到高速公路所在直线 的距离分别为 , , ,要在高速公路上E、F之间建一个出口Q,使A、B两城镇到Q的距离之和最短,在图中画出点Q所在位置,并求出这个最短距离.
 17. 如图, 三个顶点的坐标分别为A(-2,2), , .
17. 如图, 三个顶点的坐标分别为A(-2,2), , .
⑴画出 关于y轴对称的 ;
⑵在y轴上画出点Q,使 最小.并直接写出点Q的坐标.
18. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小. 19. 如图,等边 的边长为 , 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为多少?
19. 如图,等边 的边长为 , 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为多少?
四、综合题
-
20. 如图,在平面直角坐标系中,的顶点都在网格格点上,点坐标为 .
 (1)、作出关于轴对称的 , 并写出点的坐标;(2)、在轴上找一点 , 使得最短,并写出点的坐标.21. 在平面直角坐标系中,△ABC的三个顶点分别是A(2,4),B(1,1),C(3,2).
(1)、作出关于轴对称的 , 并写出点的坐标;(2)、在轴上找一点 , 使得最短,并写出点的坐标.21. 在平面直角坐标系中,△ABC的三个顶点分别是A(2,4),B(1,1),C(3,2). (1)、画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标:A1( , );(2)、求△ABC的面积;(3)、在y轴上找一点P(保留作图痕迹),使PA+PB的值最小,请直接写出点P的坐标:P( , ).22. 如图,在正方形网格中点均为格点,按要求作图(保留作图痕迹,不写作法):
(1)、画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标:A1( , );(2)、求△ABC的面积;(3)、在y轴上找一点P(保留作图痕迹),使PA+PB的值最小,请直接写出点P的坐标:P( , ).22. 如图,在正方形网格中点均为格点,按要求作图(保留作图痕迹,不写作法): (1)、作出关于直线l的对称图形;(2)、在直线l上找一点D,使最小.23. 如图,在Rt△ABC中,∠ACB=90,∠A=30°,AC= , BC=6,CD平分∠ACB交斜边AB于点D,动点P从点C出发,沿折线CA―AD向终点D运动.
(1)、作出关于直线l的对称图形;(2)、在直线l上找一点D,使最小.23. 如图,在Rt△ABC中,∠ACB=90,∠A=30°,AC= , BC=6,CD平分∠ACB交斜边AB于点D,动点P从点C出发,沿折线CA―AD向终点D运动. (1)、点P在CA上运动的过程中,当CP=时,△CPD与△CBD的面积相等;(直接写出答案)(2)、点P在折线CA―AD上运动的过程中,若△CPD是等腰三角形,求∠CPD的度数;(3)、若点E是斜边AB的中点,当动点P在CA上运动时,线段CD所在直线上存在另一动点M,使两线段MP、ME的长度之和,即MP+ME的值最小,则此时CP的长度= . (直接写出答案)
(1)、点P在CA上运动的过程中,当CP=时,△CPD与△CBD的面积相等;(直接写出答案)(2)、点P在折线CA―AD上运动的过程中,若△CPD是等腰三角形,求∠CPD的度数;(3)、若点E是斜边AB的中点,当动点P在CA上运动时,线段CD所在直线上存在另一动点M,使两线段MP、ME的长度之和,即MP+ME的值最小,则此时CP的长度= . (直接写出答案)