（人教版）2023-2024学年八年级数学上册 13.2 作轴对称图形期中专项复习

试卷更新日期：2023-10-11 类型：复习试卷

进入出卷网下载

一、选择题

1. 把 $△ A B C$ 各顶点的横坐标都乘以-1，纵坐标都不变，所得图形是下列答案中的（）

A、 B、 C、 D、

查看试题解析
2. 如图，在 $3 \times 3$ 的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的 $△ A B C$ 为格点三角形，在图中最多能画出（）个格点三角形与 $△ A B C$ 成轴对称.

A、6 B、5 C、4 D、3

查看试题解析
3. 如图是2×5的正方形网格，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形.则在网格中，能画出且与△ABC成轴对称的格点三角形一共有（）个.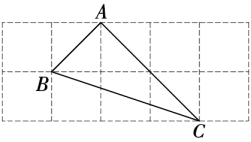

A、1 B、2 C、3 D、4

查看试题解析
4. 已知△ABC为直角坐标系中任意位置的一个三角形，现将△ABC的各顶点横坐标乘以-1，得到△A₁B₁C₁ ，则它与△ABC的位置关系是（）

A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、关于直线y=x对称

查看试题解析
5. 如图，在 $4 \times 4$ 的正方形网格中，有5个小正方形已被涂黑（图中阴影部分），若在其余网格中再涂黑一个小正方形，使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形，则可涂黑的小正方形共有（）个．

A、2 B、3 C、4 D、5

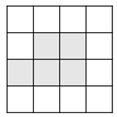查看试题解析
6. 小明作点 $A (1 ， 2)$ 关于x轴的对称点 $A_{1}$ ，再作 $A_{1}$ 关于y轴的对称点 $A_{2}$ ，则 $A_{2}$ 的坐标为（）

A、 $(1 ， 2)$ B、 $(- 1 ， - 2)$ C、 $(- 1 ， 2)$ D、 $(1 ， - 2)$

查看试题解析
7. 在平面直角坐标系中，若点A（m ， 2）与点B（3，n）关于y轴对称，则m ， n的值分别为（）

A、－3，－2 B、－3，2 C、3，－2 D、3，2

查看试题解析
8. 在平面直角坐标系中，把△ABC先沿x轴翻折，再向右平移3个单位₁B₁C₁ ，把这两步操作规定为翻移变换，如图，已知等边三角形ABC的顶点B（1，1），（3，1）．把△ABC经过连续3次翻移变换得到△A₃B₃C₃ ，则点A的对应点A₃的坐标是（）

A、（5，- $\sqrt{3}$ ） B、（8，1+ $\sqrt{3}$ ） C、（11，-1- $\sqrt{3}$ ） D、（14，1+ $\sqrt{3}$ ）

查看试题解析
9. 已知点 $P_{1} (a ， 3)$ 和 $P_{2} (2 ， b)$ 关于x轴对称，则 ${(a + b)}^{2022}$ 的值是（）

A、0 B、 $- 1$ C、1 D、 $5^{2022}$

查看试题解析
10. 在平面直角坐标系中，点 $P (a ， 3)$ 与点 $Q (- 2 ， b)$ 关于 $x$ 轴对称，则 $a - b$ 的值为（）

A、1 B、-1 C、5 D、-5

查看试题解析

二、填空题

11. 如图，在平面直角坐标系xOy中，△OCD可以看作是△ABO经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABO得到△OCD的过程：.

查看试题解析
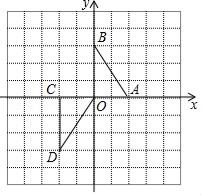12. 如图，在 $3 \times 3$ 的正方形网格中，其中有三格被涂黑，若在剩下的6个空白小方格中涂黑其中1个，使所得的图形是轴对称图形，则可选的那个小方格的位置有种.

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，点 $A (2 ， - 3)$ 关于 $x$ 轴对称的点 $B$ 的坐标是

查看试题解析
14. 点 $P (m + 2 ， 2 m - 5)$ 在x轴上，则m的值为．

查看试题解析
15. 在平面直角坐标系 $x O y$ 中，点 $A (- 3 ， 4)$ 和点 $B (3 ， 4)$ 关于轴对称．

查看试题解析

三、解答题

16. 已知点 $A (a ， - 3)$ 与点 $B (5 ， b)$ 关于x轴对称，求 $a + b$ 的立方根．

查看试题解析
17. $△ A B C$ 在平面直角坐标系中的位置如图所示，A、B、C三点在格点上，点B的坐标为 $(1 ， 1)$ ．

（ 1 ）作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

（ 2 ）作出 $△ A_{1} B_{1} C_{1}$ 关于y轴对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $A_{2}$ 的坐标，

查看试题解析
18. 在下图给出一个图案的左半部分，其中虚线是这个图案的对称轴．请你画出这个图案的右半部分，使它组成一个完整的图案．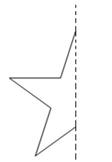

查看试题解析
19. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为 $A (- 4 ， 5) ， C (- 1 ， 3)$ ．
（ 1 ）请在如图所示的网格内作出x轴、y轴；
（ 2 ）请作出∆ABC关于y轴对称的∆ $A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标；
（ 3 ）求出∆ $A_{1} B_{1} C_{1}$ 的面积．

查看试题解析

四、综合题

20. 如图，在边长为1的小正方形所组成的网格上，每个小正方形的顶点都称为“格点”， $△ A B C$ 的顶点都在格点上，用直尺完成下列作图：

(1)、作出 $△ A B C$ 关于直线 $M N$ 的对称图形；

(2)、 $△ A B C$ 的面积为．

查看试题解析
21. 如图，在正方形网格中，每个小正方形的边长为1，格点 $△ A B C$ 的顶点A，B的坐标分别为 $(- 2 ， 1)$ ， $(0 ， 3)$ .
⑴请在图中建立适当的直角坐标系.
⑵画出 $△ A B C$ 关于x轴对称的 $△ A^{'} B^{'} C^{'}$ ，并直接写出点 $C^{'}$ 的坐标.

查看试题解析
22. 在直角坐标系平面内，已知点A的坐标为 $(- 1 ， 4)$ ，点B的位置如图所示，点C是第一象限内一点，且点C到 $x$ 轴的距离是3，到 $y$ 轴的距离是4．

(1)、写出图中点B的坐标：；在图中描出点C ，并写出C的坐标：；

(2)、画出 $△ A B O$ 关于 $y$ 轴的对称图形 $△ A^{'} B^{'} O$ ，并联结 $A^{'} B$ ， $B B^{'}$ 、 $B^{'} C$ ， $A^{'} C$ ，那么四边形 $A^{'} B B^{'} C$ 的面积等于．

查看试题解析
23. 已知点 $A (3 x - 5 ， 6 - 2 x)$ ， B点坐标为 $(1 ， - 2)$ ．

(1)、若点A和点B关于x轴对称，求A点坐标；

(2)、若直线 $A B ∥ x$ 轴，求A点坐标．

查看试题解析

（人教版）2023-2024学年八年级数学上册 13.2 作轴对称图形 期中专项复习

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 13.2 作轴对称图形期中专项复习