浙江省金华市金东区2023-2024学年八年级上册数学开学试卷

试卷更新日期：2023-10-11 类型：开学考试

进入出卷网下载

一、仔细选一选（本大题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不得分．）

1. 要调查某校七年级学生周日的睡眠时间，选取调查对象最合适的是（　　）

A、选取七年级一个班级的学生 B、选取50名七年级男生 C、选取50名七年级女生 D、随机选取50名七年级学生

查看试题解析
2. 航空工业作为“现代工业之花”，对航空材料的选取有极高的要求．我国科研人员攻克技术难题，已经能将航空发动机风扇叶片关键曲面轮廓误差控制在0.000007m以内.0.000007用科学记数法表示为（）

A、7×10^-6 B、7×10^-5 C、0.7×10^-6 D、0.7×10^-5

查看试题解析
3. 计算a²+3a²的结果是（）

A、3a² B、4a² C、3a⁴ D、4a⁴

查看试题解析
4. ${\begin{cases} x = 5 \\ y = 3 \end{cases}$ 是下面哪个二元一次方程的解（）

A、y＝-x+2 B、x-2y＝1 C、x＝y-2 D、2x-3y＝1

查看试题解析
5. 若a＞b，则下列式子中一定成立的是（）

A、a﹣2＜b﹣2 B、 $\frac{a}{2}$ ＞ $\frac{b}{2}$ C、2a＞b D、3﹣a＞3﹣b

查看试题解析
6. 一个直尺和一个含45°的直角三角板按如图方式叠合在一起（三角板的两个顶点分别在直尺的边上），若∠1＝20°，则∠2的度数是（）

A、20° B、65° C、70° D、75°

查看试题解析
7. 下列多项式中能用完全平方公式分解的是（）

A、x²-x+1 B、1-2x+x² C、a²+a+ $\frac{1}{2}$ D、-a²+b²-2ab

查看试题解析
8. 如图， $△ A B C$ 以每秒 $2 c m$ 的速度沿着射线 $B C$ 向右平移，平移2秒后所得图形是 $△ D E F$ ，如果 $A D = 2 C E$ ，那么 $B C$ 的长是（　　）

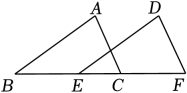A、4 B、6 C、8 D、9

查看试题解析
9. 如图，点B，F，E，D共线，∠B＝∠D，BE＝DF，添加一个条件，不能判定△ABF≌△CDE的是（）

A、AF∥CE B、∠A＝∠C C、AF＝CE D、AB＝CD

查看试题解析
10. 为迎接亚运，某校购买了一批篮球和足球，已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元，设足球的单价为x元，根据题意，下列方程正确的是（）

A、 $\frac{5000}{x} = 2 \times \frac{4000}{30 + x}$ B、 $\frac{5000}{x} = 2 \times \frac{4000}{30 - x}$ C、 $2 \times \frac{5000}{x} = \frac{4000}{30 + x}$ D、 $2 \times \frac{5000}{x} = \frac{4000}{30 - x}$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 分解因式：2m²﹣18= ．

查看试题解析
12. 计算： $\frac{2 a + b}{a - b}$ + $\frac{3 b}{b - a}$ 的结果是．

查看试题解析
13. 为推广全民健身运动，某单位组织员工进行爬山比赛，其中青年组有20人，中年组有17人，老年组有13人，则中年组的频率是．

查看试题解析
14. 满足方程组 ${\begin{array}{l} 4 x + 2 y = 3 m \\ 3 x + y = m + 2 \end{array}$ 的x，y互为相反数，则m =.

查看试题解析
15. 如图，将长方形 $A B C D$ 沿 $E F$ 翻折，点 $B$ 的对应点 $G$ 恰好落在 $D C$ 边上，若 $∠ 1 = 20 °$ ，则 $∠ D E F$ 的度数为．

查看试题解析
16. 在△ABC中，AB＝AC，且过△ABC某一顶点的直线可将△ABC分成两个等腰三角形，则∠BAC的度数为．

查看试题解析

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

17. 计算：

(1)、（16xy²-4xy）÷4xy；

(2)、（a+3）（a-3）+a（1-a）．

查看试题解析
18. 解方程（组）：

(1)、 ${\begin{cases} x + 2 y = 8 \\ 3 x + y = 9 \end{cases}$ ；

(2)、 $\frac{2 x}{x + 1} - 2 = \frac{3}{x^{2} - 1}$ ．

查看试题解析
19. 解不等式（组）：

(1)、5x-2＞x+1；

(2)、 ${\begin{cases} 4 (x + 1) < 7 x + 13 \\ 2 x - 4 < \frac{x - 8}{3} \end{cases}$ ．

查看试题解析
20. 在6×5的方格纸中，请按下列要求画出格点三角形（顶点都在格点上）．

⑴在图1中画出将△ABC向右平移3个单位后得到的△A₁B₁C₁；

⑵在图2中画出△ABC关于直线MN成轴对称的△A₂B₂C₂ ．

查看试题解析
21. 学校就“我最喜爱的课外读物”从文学、艺术，科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了多少名同学；

(2)、求条形统计图中m，n的值；

(3)、扇形统计图中，求艺术类读物所在扇形的圆心角的度数.

查看试题解析
22. 如图，点 $B$ 、 $E$ 、 $C$ 、 $F$ 在同一条直线上， $A C$ 与 $D E$ 相交于点 $O$ ， $A C ∥ D F$ ， $A B ∥ D E$ ， $B E = C F$ ．

(1)、求证： $A C = D F$ ；

(2)、若 $∠ E O C = 80 °$ ， $∠ F = 36 °$ ，求 $∠ B$ 的度数．

查看试题解析

23. 根据以下素材，探索完成任务．

如何设计板材裁切方案？
素材1	图1中是一张学生椅，主要由靠背、座垫及铁架组成．经测量，该款学生椅的靠背尺寸为40cm×15cm，座垫尺寸为40cm×35cm．图2是靠背与座垫的尺寸示意图．
素材2	因学校需要，某工厂配合制作该款式学生椅．经清点库存时发现，工厂仓库已有大量的学生椅铁架，只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫．已知该板材长为240cm，宽为40cm．（裁切时不计损耗）

我是板材裁切师

(1)、任务一：拟定裁切方案

若要不造成板材浪费，请你设计出一张该板材的所有裁切方法．

方法一：裁切靠背16张和座垫0张．

方法二：裁切靠背张和坐垫张．

方法三：裁切靠背张和坐垫张．

(2)、任务二：确定搭配数量

若该工厂购进50张该型号板材，能制作成多少张学生椅？

(3)、任务三：解决实际问题

现需要制作700张学生椅，该工厂仓库现有1张座垫和11张靠背，还需要购买该型号板材多少张（恰好全部用完）？并给出一种裁切方案．

查看试题解析

24. 在△ABC中，AB＝BC＝2，∠ABC＝90°，BP是AC边上的高线，将一块三角板的直角顶点放在点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AB、BC于D、E两点．图1和图2是旋转三角板得到的图形中的两种情况．

(1)、求证：BP＝CP；

(2)、猜想线段PD与PE之间的数量关系，并结合图1证明你的结论；

(3)、在三角板绕点P旋转的整个过程中，当△PEC为等腰三角形时，求BE的长．

查看试题解析