浙江省金衢山五校联盟2023-2024学年九年级上册数学9月月考试卷

试卷更新日期：2023-10-11 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列函数中，是二次函数的有（）
$① y = 3 (x - 1)^{2} + 1$ ； $② y = x + \frac{1}{x}$ ； $③ y = 8 x^{2} + 1$ ； $④ y = 3 x^{3} + 2 x^{2}$ ．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
2. 对于二次函数 $y = 3 (x + 4)^{2}$ ，其图象的顶点坐标为（）

A、 $(0 ， 4)$ B、 $(0 ， - 4)$ C、 $(4 ， 0)$ D、 $(- 4 ， 0)$

查看试题解析
3. 将抛物线 $y = - \frac{1}{3} (x - 2)^{2}$ 向右平移 $1$ 个单位，再向下平移 $2$ 个单位后，得到的抛物线解析式为（）

A、 $y = - \frac{1}{3} (x - 1)^{2} + 2$ B、 $y = - \frac{1}{3} (x - 1)^{2} - 2$ C、 $y = - \frac{1}{3} (x - 3)^{2} + 2$ D、 $y = - \frac{1}{3} (x - 3)^{2} - 2$

查看试题解析
4. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A (- 4 ， 0)$ 和原点，且顶点在第二象限 $.$ 下列说法正确的是（）

A、 $a > 0$ B、当 $x > - 1$ 时， $y$ 的值随 $x$ 值的增大而减小 C、 $b^{2} - 4 a c < 0$ D、函数值有最小值 $4 a - 2 b + c$

查看试题解析
5. 如图是抛物线形拱桥，当拱顶离水面 $2$ 米时，水面宽 $6$ 米，则当水面宽 $8$ 米时，水面下降了（）

A、 $\frac{32}{9}$ 米 B、 $2$ 米 C、 $\frac{16}{9}$ 米 D、 $\frac{14}{9}$ 米

查看试题解析
6. 某种品牌的服装进价为每件 $150$ 元，当售价为每件 $210$ 元时，每天可卖出 $20$ 件，现需降价处理，且经市场调查：每件服装每降价 $2$ 元，每天可多卖出 $1$ 件．在确保盈利的前提下，若设每件服装降价 $x$ 元，每天售出服装的利润为 $y$ 元，则 $y$ 与 $x$ 的函数关系式为（）

A、 $y = - \frac{1}{2} x^{2} + 10 x + 1200 (0 < x < 60)$ B、 $y = - \frac{1}{2} x^{2} - 10 x + 1250 (0 < x < 60)$ C、 $y = - \frac{1}{2} x^{2} + 10 x + 1250 (0 < x < 60)$ D、 $y = - \frac{1}{2} x^{2} + 10 x + 1250 (x \leq 60)$

查看试题解析
7. 已知抛物线 $y = - x^{2} + 2 x + c$ ，若点 $(0 ， y_{1}) (1 ， y_{2}) (3 ， y_{3})$ 都在该抛物线上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{3} > y_{1} > y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{3} > y_{2} > y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
8. 二次函数 $y = - x^{2} + b x + c$ 的图象的最高点是 $(- 1 ， - 3)$ ，则 $b$ ， $c$ 的值分别是（）

A、 $2$ ， $4$ B、 $2$ ， $- 4$ C、 $- 2$ ， $4$ D、 $- 2$ ， $- 4$

查看试题解析
9. 如图，正方形 $A B C D$ 的边长为 $1$ ， $E$ 、 $F$ 、 $G$ 、 $H$ 分别为各边上的点，且 $A E = B F = C G = D H$ ，设小正方形 $E F G H$ 的面积为 $y$ ， $A E$ 为 $x$ ，则 $y$ 关于 $x$ 的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 二次函数 $y = - x^{2} + b x + c$ 的图象如图所示，下列几个结论： $①$ 对称轴为直线 $x = 2$ ； $②$ 当 $y \geq 0$ 时， $x < 0$ 或 $x > 4$ ； $③$ 函数表达式为 $y = - x^{2} + 4 x$ ； $④$ 当 $x \leq 0$ 时， $y$ 随 $x$ 的增大而增大．其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 二次函数 $y = a (x - m)^{2}$ 的图象如图，已知 $a = \frac{1}{2}$ ， $O A = O C$ ，则该抛物线的解析式为 $. ($ 用顶点式表示 $)$

查看试题解析
12. 点 $P (a ， 9)$ 在函数 $y = 4 x^{2} - 3$ 的图象上，则代数式 $(2 a + 3) (2 a - 3)$ 的值等于 .

查看试题解析
13. 已知 $y$ 关于 $x$ 的二次函数 $y = - x^{2} + (m - 1) x + m$ ，无论 $m$ 取何值，函数图象恒过定点 $A$ ，则点 $A$ 的坐标为．

查看试题解析
14. 在同一直角坐标系中，已知函数 $y_{1} = x^{2} + 2 x + c$ ， $y_{2} = k x + 2$ （k为不等于零的常数）.若函数 $y_{2}$ 的图象经过 $y_{1}$ 的图象的顶点，则k，c之间的数量关系为.

查看试题解析

15. 如图所示的是卡塔尔世界杯足球比赛中某一时刻的鹰眼系统预测画面

(

图

1)

和截面示意图

(

图

2)

，足球的飞行轨迹可看成抛物线，足球离地面的高度

h (m)

与足球被踢出后经过的时间

t (s)

之间的关系的部分数据如表：则该运动员踢出的足球在第

s

落地．

$t / s$	$0$	$1$	$2$	$3$	$\dots$
$h / m$	$0$	$\frac{7}{8}$	$\frac{3}{2}$	$\frac{15}{8}$	$\dots$

查看试题解析

16. 如图，在平面直角坐标系中，二次函数 $y = x^{2} + 2 x - 3$ 的图象与坐标轴相交于 $A$ ， $B$ ， $C$ 三点，连接 $A C$ ， $B C .$ 已知点 $E$ 坐标为 $(\frac{1}{2} ， 0)$ ，点 $D$ 在线段 $A C$ 上，且 $A D = \frac{\sqrt{2}}{2} .$ 则四边形 $B C D E$ 面积的大小为．

查看试题解析

三、解答题（本大题共8小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）

17. 计算：

(1)、 $(x - 1 - \frac{8}{x + 1}) \div \frac{3 x - x^{2}}{x^{2} + x}$ ；

(2)、 $x (x + 6) = 8 (x + 3)$ ．

查看试题解析
18. 如图 $1$ 是某公园人工湖上的一座拱桥的示意图，其截面形状可以看作是抛物线的一部分 $.$ 经测量拱桥的跨度 $A B$ 为 $12$ 米，拱桥顶面最高处到水面的距离 $C D$ 为 $4$ 米．

(1)、在边长为 $1$ 的正方形网格中建立适当的平面直角坐标系，根据已知数据描出点 $A$ ， $B$ ， $C$ ，并用平滑曲线连接；

(2)、结合(1)中所画图象，求出该抛物线的表达式；

(3)、现有一游船 $($ 截面为矩形 $)$ 宽度为 $4$ 米，顶棚到水面的高度为 $2.8$ 米 $.$ 当游船从拱桥正下方通过时，为保证安全，要求顶棚到拱桥顶面的距离应大于 $0.5$ 米，请判断该游船能否安全通过此拱桥．

查看试题解析

19. 供销社作为国家实施“乡村振兴”战略的中坚力量，可以帮助农民分配协调农产品，推动全国统一大市场尽快构建完成，给老百姓带来真正的实惠

.

某供销社指导农民生产和销售当地特产，对该特产的产量与市场需求，成本与售价进行了一系列分析，发现该特产产量

y_{产 量} (

单位：吨

)

是关于售价

x (

单位：元

/

千克

)

的一次函数，即

y_{产 量} = 200 x - 100

；而市场需求量

y_{需 求} (

单位：吨

)

是关于售价

x (

单位：元

/

千克

)

的二次函数，部分对应值如表．

售价 $x ($ 元 $/$ 千克 $)$	$\dots$	$2$	$3$	$4$	$5$	$\dots$
需求量 $y_{需求} ($ 吨 $)$	$\dots$	$1020$	$1020$	$980$	$900$	$\dots$

同时还发现该特产售价 $x ($ 单位：元 $/$ 千克 $)$ ，成本 $z ($ 单位：元 $/$ 千克 $)$ 随着时间 $t ($ 月份 $)$ 的变化而变化，其函数解析式分别为 $x = t + 1$ ， $z = \frac{1}{8} t^{2} + \frac{3}{2}$ ．

(1)、直接写出市场需求量

y_{需 求}

关于售价

x

的函数解析式

(

不要求写出自变量取值范围

)

；

(2)、哪个月份出售这种特产每千克获利最大？最大值是多少？

(3)、供销社发挥职能作用，避免浪费，指导农民生产，若该特产的产量与市场需求量刚好相等，求此时出售全部特产获得的总利润．

查看试题解析

20. 如图，抛物线 $y = - x^{2} + 2 x + c$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，若直线 $y = k x + b (k \neq 0)$ 与抛物线交于点 $A$ 、 $C$ 两点，已知 $A (- 1 ， 0)$ ， $C (2 ， m)$ ．

(1)、求直线 $A C$ 的函数表达式；

(2)、若将直线 $A C$ 沿 $y$ 轴的正方向向上平移 $n$ 个单位长度后，与抛物线只有一个公共点，求此时 $n$ 的值．

查看试题解析
21.

(1)、[回归教材]已知一元二次方程 $a x^{2} + b x + c = 0 (a$ 、 $b$ 、 $c$ 为常数， $a \neq 0)$ 的两个实数解为 $x_{1}$ ， $x_{2}$ ，则有 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a} .$ 这个结论课本上称为一元二次方程根与系数的关系，因为是法国数学家韦达发现的，人们又称它为“韦达定理” $.$ 请你证明这个定理．

(2)、[夯实基础]若一元二次方程 $3 x^{2} - 9 x - 8 = 0$ 的两个实数解为 $x_{1}$ 、 $x_{2}$ ，求 $3 x_{1}^{2} + 9 x_{2} + 5$ 的值．

(3)、[拓展应用]若关于 $x$ 的一元二次方程 $x^{2} - (2 a + 1) x + a^{2} + 1 = 0$ 的两个实数解为 $x_{1}$ 、 $x_{2}$ ，求 $x_{1}^{2} + x_{2}^{2}$ 的最小值．

查看试题解析
22. 为研究某种化学试剂的挥发情况，某研究团队在两种不同的场景下做对比实验，收集了该试剂挥发过程中剩余质量 $y ($ 克 $)$ 随时间 $x ($ 分钟 $)$ 变化的数据 $(0 \leq x \leq 20)$ ，并分别绘制在直角坐标系中，如图所示．

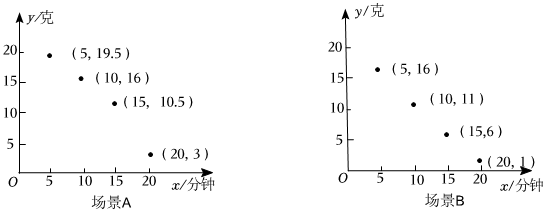(1)、从 $y = a x + 21 (a \neq 0)$ ， $y = \frac{k}{x} (k \neq 0)$ ， $y = - 0.04 x^{2} + b x + c$ 中，选择适当的函数模型分别模拟两种场景下 $y$ 随 $x$ 变化的函数关系，并求出相应的函数表达式；

(2)、查阅文献可知，该化学试剂发挥作用的最低质量为 $3$ 克 $.$ 在上述实验中，该化学试剂在哪种场景下发挥作用的时间更长？

查看试题解析

23.

【阅读理解】：

关于 $x$ 的函数 $y = m x - 2 m - 3 (m$ 为常数，且 $m \neq 0)$ ，经过某个定点，请求出定点的坐标．

方法一：先将等式化为 $(x - 2) m = y + 3$ 的形式，再根据 $0 m = 0$ 时有 $m$ 无数多个解，求得定点的坐标为 $(2 ， - 3)$ ；

方法二：当 $m = 1$ 时， $y = x - 5$ ；当 $m = 2$ 时， $y = 2 x - 7$ ；

解方程组 ${\begin{array}{l} y = x - 5 \\ y = 2 x - 7 \end{array}$ 解得 ${\begin{array}{l} x = 2 \\ y = - 3 \end{array}$ ，

$∴$ 求得定点的坐标为 $(2 ， - 3)$

(1)、【模仿练习】

关于 $x$ 的二次函数 $y = m x^{2} + (2 m + 1) x + 1 ($ 为常数，且 $m \neq 0)$ ，是否经过定点，如果是，请选择一种方法求出定点的坐标；如果不是，请说明理由．

(2)、【尝试应用】

某“数学兴趣小组”根据学习函数的经验，对函数 $y = - (x - 1) (| x | - 3)$ 的图象和性质进行了探究，探究过程如下，请补充完整：

①计算 $x$ 与 $y$ 的几组对应值，其中 $m =$ ▲ ；

②列表如下：

$x$	$\dots$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$	$4$	$\dots$
$y$	$\dots$	$5$	$0$	$- 3$	$m$	$- 3$	$0$	$1$	$0$	$- 3$	$\dots$

如图，在直角坐标系中用描点法画出了函数 $y = - (x - 1) (| x | - 3)$ 这个图象；

③若直线 $y = t x - 2 t + 2$ 与函数 $y = - (x - 1) (| x | - 3) (2 < x \leq 4)$ 的图象只有一个交点，请结合函数图象，求出 $t$ 的取值范围．

查看试题解析

24. “距离”是数学研究的重要对象，如我们所熟悉的两点间的距离 $.$ 现在我们定义一种新的距离：已知 $P (a ， b)$ ， $Q (c ， d)$ 是平面直角坐标系内的两点，我们将 $| a - c | + | b - d |$ 称作 $P$ ， $Q$ 间的“ $L$ 型距离”，记作 $L (P ， Q)$ ，即 $L (P ， Q) = | a - c | + | b - d |$ ．
已知二次函数 $y_{1}$ 的图象经过平面直角坐标系内的 $A$ ， $B$ ， $C$ 三点，其中 $A$ ， $B$ 两点的坐标为 $A (- 1 ， 0)$ ， $B (0 ， 3)$ ，点 $C$ 在直线 $x = 2$ 上运动，且满足 $L (B ， C) \leq B C$ ．

(1)、求 $L (A ， B)$ ；

(2)、求抛物线 $y_{1}$ 的表达式；

(3)、已知 $y_{2} = 2 t x + 1$ 是该坐标系内的一个一次函数．
$①$ 若 $D$ ， $E$ 是 $y_{2} = 2 t x + 1$ 图象上的两个动点，且 $D E = 5$ ，求 $△ C D E$ 面积的最大值；
$②$ 当 $t \leq x \leq t + 3$ 时，若函数 $y = y_{1} + y_{2}$ 的最大值与最小值之和为 $8$ ，求实数 $t$ 的值．

查看试题解析