广东省汕头市某重点中学2023-2024学年度九年级上册数学第一次月考试卷
试卷更新日期:2023-10-11 类型:月考试卷
一、选择题:(每小题3分,共30分)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
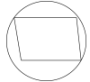 B、
B、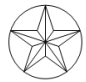 C、
C、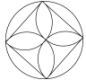 D、
D、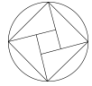 2. 方程x2-2 x+2=0的根的情况为( )A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根3. 点P(-2,3)关于原点的对称点Q的坐标为( )A、(2,-3) B、(2,3) C、(3,-2) D、(-2,-3)4. 抛物线y=3(x-7)2+5的顶点坐标是( )A、(7,5) B、(7,-5) C、(-7,5) D、(-7,-5)5. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送2970张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=2970 B、x(x-1)=2970 C、2x(x+1)=2970 D、2x(x-1)=29706. 用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )A、(x-1)2=4 B、(x+1)2=4 C、(x-1)2=16 D、(x+1)2=167. 已知抛物线y=x2-2x+3,A(-1,y1),B(2,y2)C(4,y3)是抛物线上的三个点,则y1 , y2 , y3 , 从小到大排列是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y2<y3<y18. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,∠AOB'的度数是( )
2. 方程x2-2 x+2=0的根的情况为( )A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根3. 点P(-2,3)关于原点的对称点Q的坐标为( )A、(2,-3) B、(2,3) C、(3,-2) D、(-2,-3)4. 抛物线y=3(x-7)2+5的顶点坐标是( )A、(7,5) B、(7,-5) C、(-7,5) D、(-7,-5)5. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送2970张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=2970 B、x(x-1)=2970 C、2x(x+1)=2970 D、2x(x-1)=29706. 用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )A、(x-1)2=4 B、(x+1)2=4 C、(x-1)2=16 D、(x+1)2=167. 已知抛物线y=x2-2x+3,A(-1,y1),B(2,y2)C(4,y3)是抛物线上的三个点,则y1 , y2 , y3 , 从小到大排列是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y2<y3<y18. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,∠AOB'的度数是( ) A、25° B、30° C、35° D、40°9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( )
A、25° B、30° C、35° D、40°9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( ) A、点A B、点B C、点C D、点D10. 如图,垂直于x轴的直线AB分别与抛物线C1:和抛物线C2:交于A,B两点,过点A作CD//x轴分别与y轴和抛物线C2交于点C,D,过点B作EF//x轴分别与y轴和抛物线C1交于点E,F,则的值为( )
A、点A B、点B C、点C D、点D10. 如图,垂直于x轴的直线AB分别与抛物线C1:和抛物线C2:交于A,B两点,过点A作CD//x轴分别与y轴和抛物线C2交于点C,D,过点B作EF//x轴分别与y轴和抛物线C1交于点E,F,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:(每小题3分,共18分)
-
11. 方程x2=4x的解为12. 抛物线y=(x+2)2+3先向右平移3个单位,再向下平移2各单位后的解析式是13. 点A(2,3)绕着坐标原点顺时针旋转90°后对应的点的坐标是14. 下图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是
 15. 已知x为实数,且满足(x2+3x)2+2(x2+3x)-3=0,那么x2+3x的值为16. 已知二次函数,当-1≤x≤2时,函数y=mx2-2mx+2(m≠0)的最大值为y=4,则m的值是
15. 已知x为实数,且满足(x2+3x)2+2(x2+3x)-3=0,那么x2+3x的值为16. 已知二次函数,当-1≤x≤2时,函数y=mx2-2mx+2(m≠0)的最大值为y=4,则m的值是三、解答题一:(每小题6分,共18分)
-
17. 用公式法解方程:2x2-2x-1=018. 已知关于x的方程x2-2x+m-1=0有两个实数根(1)、求m的取值范围;(2)、设p是方程的一个实数根,且满(p2-2p+3)(m+4)=7足,求m的值19. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.

⑴作△ABC关于点P的中心对称图形△A1B1C1
⑵作△ABC绕着点B顺时针方向旋转90°而得到的△A2B2C2
四、解答题二:(每小题8分,共24分)
-
20. 已知关于x的方程x2+2mx+m2-4=0(1)、求证:无论m为何值,该方程总有两个不相等的实数根:(2)、若该方程的两个根为p,g,满足pg=p+g求m的值21. 菜农李伟种植的某蔬菜计划以5元/千克的单价对外批发销售,由于部分菜农盲目扩大种植,造成蔬菜滞销,李伟为了加快销售,减少损失,对价格进行两次下调后,以3.2元/千克的单价对外批发销售。(1)、求平均每次下调的百分率。(2)、如果李伟按以前的调价方案再进行一次调价,蔬菜的批发价会跌破2.5元/千克吗?22. 某电商店铺销售一种儿童服装,其进价为每件50元,现在的销售单价为每件80元,每周可卖出200件,双十二期间,商家决定降价让利促销,经过市场调查发现,单价每件降低1元,每周可多卖出20件.(1)、若想满足每周销售利润为7500元,同时尽可能让利于顾客,则应降价为多少元?(2)、销售单价应为多少元,该店铺每周销售利润最大?最大销售利润为多少元?
五、解答题三(每小题10分,共30分)
-
23. 如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当点P到达B点或Q到达C点时,两点停止移动,如果P.Q分别从A,B,同时出发,t秒钟后。
 (1)、求出△PBQ的面积:(2)、当△PBQ的面积等于8cm2时,求t的值:(3)、是否存在△PBQ的面积等于10cm?,若存在,求出t的值,若不存在,说明理由24. 阅读材料:配方法是数学中一种重要的思想方法,它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方公式的和的方法。这种方法被用到代数式的变形中,并结合非负数的意义来解决一些问题。
(1)、求出△PBQ的面积:(2)、当△PBQ的面积等于8cm2时,求t的值:(3)、是否存在△PBQ的面积等于10cm?,若存在,求出t的值,若不存在,说明理由24. 阅读材料:配方法是数学中一种重要的思想方法,它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方公式的和的方法。这种方法被用到代数式的变形中,并结合非负数的意义来解决一些问题。我们定义:一个整数能表示成a2+b2(a,b是整数)的形式,则称这个数为“完美数”
例如5是“完美数”,理由是5=22+12.
(1)、[解决问题]数53“完美数”(填是或不是)(2)、问题探究:已知x2+y2-4x+2y+5=0,则x+y=(3)、已知S=2x2+y2+2xy+12x+k(x,y,k都是整数)要使得S为“完美数”试求出符合条件的k值。25. 如图,抛物线y=-x2+bx+c经过A(4,0),C(-1,0)两点,与y轴交于点B,P为第一象限抛物线上的动点,连接AB,BC,PA,PC,PC与AB相交于点Q. (1)、求抛物线的解析式:(2)、是否存在点P,使得△ABP的面积最大,若存在,请求出点P的坐标,若不存在,说明理由.(3)、设△APQ的面积为S1 , △BCQ的面积为S2 , S1-S2=5时,求点P的坐标.
(1)、求抛物线的解析式:(2)、是否存在点P,使得△ABP的面积最大,若存在,请求出点P的坐标,若不存在,说明理由.(3)、设△APQ的面积为S1 , △BCQ的面积为S2 , S1-S2=5时,求点P的坐标.