广东省惠州三中2023-2024学年八年级上册数学开学试卷
试卷更新日期:2023-10-11 类型:开学考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 2022年北京冬奥会顺利闭幕,奥运吉祥物“冰墩墩”让我们印象深刻,在下面的 , , , 四张“冰墩墩”图片中,能由最左边的“冰墩墩”经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列实数 , , , , 中,无理数有( )A、个 B、个 C、个 D、个3. 下列调查中,适合采用抽样调查方式的是( )A、调查你所在班级同学的视力情况 B、调查黄河的水质情况 C、对旅客上飞机前的安检 D、检查神舟十五号飞船的零部件状况4. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()
2. 下列实数 , , , , 中,无理数有( )A、个 B、个 C、个 D、个3. 下列调查中,适合采用抽样调查方式的是( )A、调查你所在班级同学的视力情况 B、调查黄河的水质情况 C、对旅客上飞机前的安检 D、检查神舟十五号飞船的零部件状况4. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是() A、 B、 C、 D、6. 点 到 轴的距离为3,到 轴的距离为2,且在第一象限内,则点 的坐标为( )A、 B、 C、 D、不能确定7. 已知是整数,则自然数的最小值是( )A、 B、 C、 D、8. 方程 , 用含的代数式表示为( )A、 B、 C、 D、9. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( )
A、 B、 C、 D、6. 点 到 轴的距离为3,到 轴的距离为2,且在第一象限内,则点 的坐标为( )A、 B、 C、 D、不能确定7. 已知是整数,则自然数的最小值是( )A、 B、 C、 D、8. 方程 , 用含的代数式表示为( )A、 B、 C、 D、9. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( ) A、 B、 C、 D、10. 关于x的不等式组的整数解仅有4个,则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 关于x的不等式组的整数解仅有4个,则m的取值范围是( )A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
11. 计算: .12. 如图,将一张长方形纸片沿折叠,点、分别落在点、的位置处,若 , 则的度数是 .
 13. 如图,在大长方形中,放入个小长方形,则图中阴影部分面积为平方厘米.
13. 如图,在大长方形中,放入个小长方形,则图中阴影部分面积为平方厘米. 14. 某商品进价元,标价元出售,商家准备打折出售,但其利润率不能少于 , 则最多可打折15. 如图,在平面直角坐标系中,点 , 点第次向上跳动个单位至点 , 紧接着第次向右跳动个单位至点 , 第次向上跳动个单位,第次向左跳动个单位,第次又向上跳动个单位,第次向右跳动个单位,依此规律跳动下去,点第次跳动至点的坐标是 .
14. 某商品进价元,标价元出售,商家准备打折出售,但其利润率不能少于 , 则最多可打折15. 如图,在平面直角坐标系中,点 , 点第次向上跳动个单位至点 , 紧接着第次向右跳动个单位至点 , 第次向上跳动个单位,第次向左跳动个单位,第次又向上跳动个单位,第次向右跳动个单位,依此规律跳动下去,点第次跳动至点的坐标是 .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
-
16.(1)、解列方程组: .(2)、解不等式组: , 并求出所有整数解的和.17. 如图,已知 , , , 求证: .
 18. 如图,网格中的每个小正方形单位长度为 , 三角形经过平移后,顶点平移到了 .
18. 如图,网格中的每个小正方形单位长度为 , 三角形经过平移后,顶点平移到了 . (1)、画出平移后的三角形;(2)、求出三角形的面积.19. 已知的立方根是 , 的算术平方根是 , 的整数部分是 .(1)、求 , , 的值.(2)、求的平方根.20. 某学校开展居家体育训练,倡导学生在家开展体育锻炼返校后,校学生会随机抽取了部分学生,就“平均每天开展体育锻炼所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分:
(1)、画出平移后的三角形;(2)、求出三角形的面积.19. 已知的立方根是 , 的算术平方根是 , 的整数部分是 .(1)、求 , , 的值.(2)、求的平方根.20. 某学校开展居家体育训练,倡导学生在家开展体育锻炼返校后,校学生会随机抽取了部分学生,就“平均每天开展体育锻炼所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分:
根据上述信息,回答下列问题:
(1)、在本次随机抽取的样本中,调查的样本容量为 , ;(2)、补全频数分布直方图;(3)、如果该校共有学生人,请你估计“平均每天开展体育锻炼的时长不少于分钟”的学生大约有多少人?21. 已知关于、的方程组 .(1)、解满足不等式 , 求实数的取值范围;(2)、在(1)的条件下化简 .22. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:进价(元/个)
售价(元/个)
电饭煲
200
250
电压锅
160
200
(1)、一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?(2)、为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;(3)、在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?23. 如图 , 在平面直角坐标系中, , , 现同时将点 , 分别向上平移个单位,再向右平移个单位,分别得到点 , 的对应点 , , 且点落在轴上,连接 , .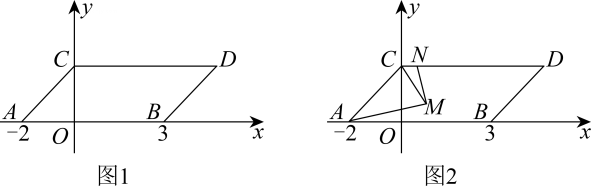 (1)、直接写出点、的坐标: ,(2)、如图 , 若点为线段的中点,点以每秒个单位长度的速度在线段上从点向点运动,运动时间为秒,则当时,求的值.(3)、如图 , 已知 , 点在轴上点的左侧,射线以的速度绕点顺时针旋转至停止,射线以的速度绕点顺时针旋转,射线、同时开始旋转,同时停止运动在射线到达之前,会与射线交于点 , 过作交于 , 则在转动过程中,的值是否会改变,如果不变请求出这个定值;如果会变,请说明理由.
(1)、直接写出点、的坐标: ,(2)、如图 , 若点为线段的中点,点以每秒个单位长度的速度在线段上从点向点运动,运动时间为秒,则当时,求的值.(3)、如图 , 已知 , 点在轴上点的左侧,射线以的速度绕点顺时针旋转至停止,射线以的速度绕点顺时针旋转,射线、同时开始旋转,同时停止运动在射线到达之前,会与射线交于点 , 过作交于 , 则在转动过程中,的值是否会改变,如果不变请求出这个定值;如果会变,请说明理由.