广东省佛山市桂城街道2022-2023学年七年级下册数学调研试卷
试卷更新日期:2023-10-11 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如所示四个图案中,不是轴对称图形的是( )A、
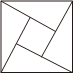 B、
B、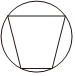 C、
C、 D、
D、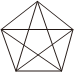 2. 下列运算中,正确的是( )A、 B、 C、 D、3. 如图,直线 , , , 则等于( )
2. 下列运算中,正确的是( )A、 B、 C、 D、3. 如图,直线 , , , 则等于( )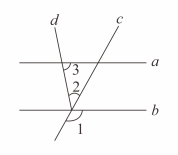 A、 B、 C、 D、4. 袋中有红球4个,白球若干个,它们只有颜色上的区别。从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )
A、 B、 C、 D、4. 袋中有红球4个,白球若干个,它们只有颜色上的区别。从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )
A、3个 B、不足3个 C、4个 D、5个或5个以上5. 已知 , 则b的值为( )A、6 B、 C、12 D、6. 如图,在四边形中, , 和的延长线交于点 , 若点使得 , 则满足此条件的点( )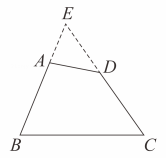 A、有且只有个 B、有且只有个 C、组成的角平分线 D、组成的角平分线所在的直线点除外7. 在277 , 355 , 544 , 633这四个数中,最大的数是( )A、277 B、355 C、544 D、6338. 在中, , , 是边上的中线,则的取值范围是( )
A、有且只有个 B、有且只有个 C、组成的角平分线 D、组成的角平分线所在的直线点除外7. 在277 , 355 , 544 , 633这四个数中,最大的数是( )A、277 B、355 C、544 D、6338. 在中, , , 是边上的中线,则的取值范围是( )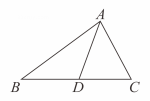 A、 B、 C、 D、无法确定9. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
A、 B、 C、 D、无法确定9. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )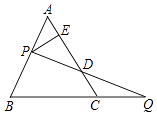 A、 B、 C、 D、10. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )
A、 B、 C、 D、10. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )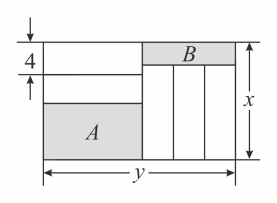
小长方形的较长边为;
阴影的较短边和阴影的较短边之和为;
若为定值,则阴影和阴影的周长和为定值;
当时,阴影和阴影的面积和为定值.
A、个 B、个 C、个 D、个二、填空题(本大题共5小题,共15.0分)
-
11. 已知纳米米,则纳米用科学记数法表示为米12. 在等腰三角形中,若 , 则 .13. 计算: .14. 如图,在等腰中, , , 是等边三角形,是的平分线上一动点,连接 , , 则的最小值为 .
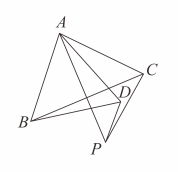 15. 如图,、、分别平分的外角、、内角 , 若 , 以下结论:;;;平分;其中正确的结论是填序号 .
15. 如图,、、分别平分的外角、、内角 , 若 , 以下结论:;;;平分;其中正确的结论是填序号 .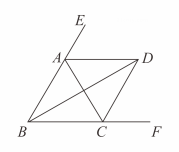
三、计算题(本大题共1小题,共8.0分)
-
16. 如图所示,自行车每节链条的长度为 , 交叉重叠部分的圆的直径为 .
 (1)、 4节链条长;(2)、节链条长;(3)、如果一辆型自行车的链条由节这样的链条组成,那么这辆自行车上链条总长度是多少?
(1)、 4节链条长;(2)、节链条长;(3)、如果一辆型自行车的链条由节这样的链条组成,那么这辆自行车上链条总长度是多少?四、解答题(本大题共7小题,共67.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 先化简,再求值: , 其中 , .18. 如图,在中, .
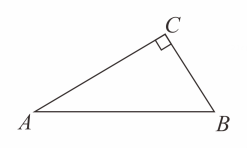 (1)、在上找一点 , 使得点到、的距离相等;尺规作图,保留痕迹(2)、在(1)上条件下,若 , 求的大小.19. 如图,以点为顶点作两个等腰直角三角形 , , , 连接 , 交于点线段和有何关系?请说明理由.
(1)、在上找一点 , 使得点到、的距离相等;尺规作图,保留痕迹(2)、在(1)上条件下,若 , 求的大小.19. 如图,以点为顶点作两个等腰直角三角形 , , , 连接 , 交于点线段和有何关系?请说明理由.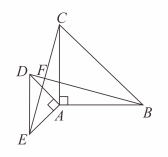 20. 已知 , 求下列各式的值:(1)、;(2)、 .21. 快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留 , 然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时间的关系如图所示.
20. 已知 , 求下列各式的值:(1)、;(2)、 .21. 快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留 , 然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时间的关系如图所示.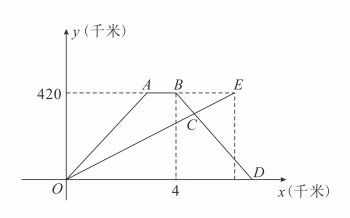 (1)、甲乙两地之间的路程为;快车的速度为;慢车的速度为;(2)、出发多少小时,快慢两车距各自出发地的路程相等;写出解答过程(3)、快慢两车出发多少小时相距写出解答过程22. 【阅读材料】配方法是数学中重要的一种思想方法它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.
(1)、甲乙两地之间的路程为;快车的速度为;慢车的速度为;(2)、出发多少小时,快慢两车距各自出发地的路程相等;写出解答过程(3)、快慢两车出发多少小时相距写出解答过程22. 【阅读材料】配方法是数学中重要的一种思想方法它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.我们定义:一个整数能表示成、是整数的形式,则称这个数为“完美数”例如,是“完美数”理由:因为 , 所以是“完美数”.
【解决问题】
(1)、数“完美数”填“是”或“不是”;(2)、【探究问题】已知 , 则;
(3)、已知、是整数,是常数 , 要使为“完美数”,试求出符合条件的值,并说明理由.(4)、【拓展结论】已知、满足 , 求的最小值.
23. 已知:如图长方形纸片中,将长方形纸片沿直线翻折,使点落在边上,记作点 , 如图 .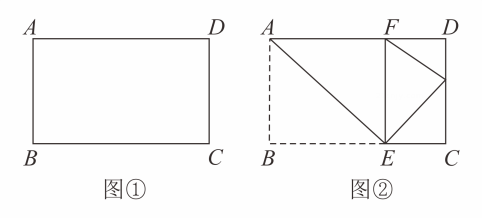 (1)、当 , 时,求线段的长度;(2)、设、 , 如果再将沿直线向右起折,使点落在射线上,记作点 , 若设线段 , 请根据题意画出图形,并求出的值;(3)、设 , , 沿直线向右翻折后交边于点 , 连接当时,求的值.
(1)、当 , 时,求线段的长度;(2)、设、 , 如果再将沿直线向右起折,使点落在射线上,记作点 , 若设线段 , 请根据题意画出图形,并求出的值;(3)、设 , , 沿直线向右翻折后交边于点 , 连接当时,求的值.
-