河南省郑州市巩义市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-10-11 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 若式子 $\sqrt{2 x - 4}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x \leq 2$ D、 $x \neq - 2$

查看试题解析
2. 小华用火柴棒摆直角三角形，已知他摆两条直角边分别用了6根和8根火柴棒，那么他摆完这个直角三角形共用火柴棒（）

A、10根 B、14根 C、24根 D、30根

查看试题解析
3. 下列各命题的逆命题不成立的是（）

A、对顶角相等 B、若 $| a | = | b |$ ，则 $a = b$ C、两直线平行，内错角相等 D、如果 $a^{2} = b^{2}$ ，那么 $a = b$

查看试题解析
4. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

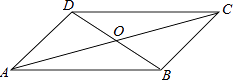A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
5. 电流通过导线时会产生热量，满足 $Q = I^{2} R t$ ，其中Q为产生的热量（单位：J），I为电流（单位：A），R为导线电阻（单位：Ω），t为通电时间（单位：s）．若导线电阻为5Ω，1s时间导线产生30J的热量，则通过的电流I为（）

A、2.4A B、 $\sqrt{6} A$ C、4.8A D、 $5 \sqrt{6} A$

查看试题解析
6. 六一儿童节来临之际，巩义市举办了以“学习二十大，争做好队员”为主题的“巩义市首届红领巾讲解员风采大赛”，7位评委分别给出某位选手了原始评分．评定该选手成绩时，从7个原始评分中去掉一个最高分、一个最低分，得到5个有效评分.5个有效评分与7个原始评分相比，这两组数据一定不变的是（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
7. 如图，在数轴上，过表示数2的点A作数轴的垂线，以点A为圆心，1长为半径画弧，交垂线于点B，再以原点O为圆心，OB长为半径画弧，交数轴于点C，则点C表示的数为（）

A、2.1 B、2.2 C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
8. 如图，一次函数 $y = m x + n$ 与正比例函数 $y = m n x$ （m，n为常数，且 $m n \neq 0$ ）的图象是（）

A、 B、 C、 D、

查看试题解析
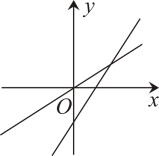9. 如图，点M是正方形ABCD内位于对角线BD下方的一点， $∠ 1 = ∠ 2$ ，则 $∠ A M B$ 为（）

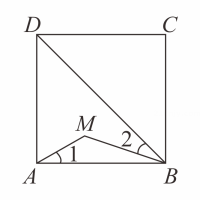A、120° B、130° C、125° D、135°

查看试题解析
10. 如图1，在菱形ABCD中，∠A＝60°，动点P从点A出发，沿折线AD→DC→CB方向匀速运动，运动到点B停止．设点P的运动路程为x，△APB的面积为y，y与x的函数图象如图2所示，则AB的长为（）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析

二、填空题（每小题3分，共15分）

11. 化简： $\sqrt{20} - \sqrt{5}$ ．

查看试题解析

12. 为提高学生对个人健康的重视，某班级举办“七步洗手法”比赛活动，小明的单项成绩如下表所示（各项成绩均按百分制计）：

项目	书面测试	实际操作	宣传展示
成绩（分）	96	98	96

若按书面测试占30%、实际操作占50%、宣传展示占20%，计算参赛个人的综合成绩（百分制），则小明的最后得分是．

查看试题解析

13. 为建设美丽乡村，需测量河两岸相对A，B两点间的距离（如图所示），可以在河外平地上选一个可以直接到达点A和点B的一点C，连接AC，BC．分别取AC，BC的中点G，H，测得 $G H = 100 m$ ，则河两岸相对A，B两点间的距离为m．

查看试题解析
14. 如图所示，一块三角尺放在一张菱形纸片上，斜边与菱形的一边平行，则 $∠ 1$ 的度数是°．

查看试题解析
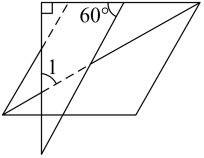15. 日常生活中常用的二维码是由许多大小相同的黑白两色小正方形按某种规律组成的一个大正方形．图1是一个 $20 \times 20$ 格式（即黑白两色小正方形个数的和是400）的二维码，左上角、左下角、右上角是三个相同的 $7 \times 7$ 格式的正方形，将其中一个放大后如图2，除这三个正方形外，图1中其他的小正方形黑色个数y与白色个数x正好满足图3所示的函数图象，则图1所示的二维码中共有个白色的小正方形．

查看试题解析

三、解答题（共8题，共75分）

16. 计算

(1)、 $\sqrt{{(- 2)}^{2}} + \sqrt{2} (1 - \sqrt{\frac{1}{2}}) + | - \sqrt{8} |$

(2)、 $\sqrt{18} - \sqrt{8} + (\sqrt{3} + 1) \times (\sqrt{3} - 1)$

查看试题解析

17. 为了让同学们了解自己的体育水平，八年级1班的体育老师对全班45名学生进行了一次体育模拟测试（得分均为整数），成绩满分为10分，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：

八年级1班体育模拟测试成绩分析表
	平均分	方差	中位数	众数
男生	____	2	8	7
女生	7.92	1.99	____	8

根据以上信息，解答下列问题：

(1)、这个班共有男生人，共有女生人；

(2)、补全八年级1班体育模拟测试成绩分析表；

(3)、你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并写出一条支持你的看法的理由．

查看试题解析

18. 小函在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：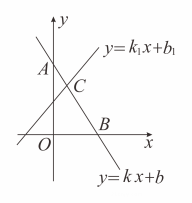

$\to_{}^{一次函数与方程的关系}$ ⑴一次函数的解析式就是一个二元一次方程；
⑵点B的横坐标是方程①的解；
⑶点C的坐标 $(x ， y)$ 中的x，y的值是方程组②的解．
$\to_{}^{一次函数与不等式的关系}$ ⑴函数 $y = k x + b$ 的函数值y大于0时，自变量x的取值范围就是不等式③的解集；
⑵函数 $y = k x + b$ 的函数值y小于0时，自变量x的取值范围就是不等式④的解集．

(1)、请将以上方框中数字序号位置应有的内容填写在下面的相应位置：
①；②；③；④；

(2)、如果点C的坐标为 $(1 ， 3)$ ，那么不等式 $k x + b \leq k_{1} x + b_{1}$ 的解集为．

查看试题解析
19. 现有如图所示的一块地（图中阴影部分）中，经测量 $∠ A D C = 90 °$ ， $A D = 4 m$ ， $C D = 3 m$ ， $A B = 13 m$ ， $B C = 12 m$ ．试求这块地的面积是多少？

查看试题解析
20. 人教版初中数学教科书八年级下册第53页设置了如下一个“思考”栏目：
思考
如图2-3，矩形ABCD的对角线AC，BD相交于点O．我们观察 $R t △ A B C$ ，在 $R t △ A B C$ 中，BO是斜边AC上的中线，BO与AC有什么关系？

经过思考与探究，从而得到了直角三角形的一个性质：直角三角形斜边上的中线等于斜边的一半．
现在，我们一起来探究这条性质的证明过程：
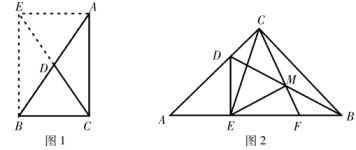
如图1：在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，CD是斜边AB上的中线．
求证： $C D = \frac{1}{2} A B$ ．
证明：延长CD至点E，使 $D E = C D$ ，连接AE，BE．
……

(1)、请你根据以上提示，结合图形，写出完整的证明过程．

(2)、定理应用：
如图2， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，D为边AC上一点， $D E ⊥ A B$ 于点E，连接BD，M为BD的中点，CM的延长线交AB于点F，连接EC，EM．
①CM与EM的数量关系是．
②若BD是 $∠ A B C$ 的平分线，且 $∠ A = 50 °$ ，则 $∠ E M B =$ °．

查看试题解析
21. 甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的函数关系如图所示，请根据图象提供的信息解答下列问题：

(1)、甲队在开挖后6小时内，每小时挖m．

(2)、当 $2 \leq x \leq 6$ 时，求 $y_{乙}$ 与x之间的函数关系式．

(3)、直接写出开挖后几小时，甲、乙两队挖的河渠的长度相差5m．

查看试题解析

22. 我市星月时代广场某衬衫专卖店购进A，B两款衬衫共100件，已知购进这100件衬衫的费用不超过7500，且其中A款衬衫不少于65件，它们的进价和售价如下表所示：

衬衫款式	进价（元/件）	售价（元/件）
A	80	120
B	60	90

其中购进A款衬衫为x件，如果购进的A，B两款衬衫全部销售完，根据表中信息，解答下列问题．

(1)、求获取总利润y元与购进A款衬衫x件的函数关系式，并写出x的取值范围；

(2)、该店对A款衬衫以每件优惠

a (0 < a < 20)

元的售价进行优惠促销活动，B款衬衫售价不变，那么该店应如何分配A，B两款衬衫的进货量，才能使总利润最大？

查看试题解析

23. 综合与实践课上，李老师让同学们以“旋转”为主题展开探究．

【问题情境】

如图①，在矩形ABCD中， $A B = 3$ ， $A D = 4$ ．将边AB绕点A逆时针旋转 $(0 ° < θ < 180 °)$ 得到线段AE，过点E作 $E F ⊥ A E$ 交直线BC与点F．

【猜想证明】

(1)、当 $θ = 90 °$ 时，四边形ABFE的形状为；（直接写出答案）

(2)、如图②，当 $θ = 45 °$ 时，连接DE，求此时 $△ A D E$ 的面积；

(3)、【能力提升】
在【问题情境】的条件下，是否存 $θ$ ，使点F，E，D三点共线？若存在，请直接写出此时BF的长度；若不存在，请说明理由．

查看试题解析