河南省郑州市巩义市2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-10-11 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的．

1. 9的平方根是（）

A、 $\pm 3$ B、 $- 3$ C、3 D、81

查看试题解析
2. 点 $P (3 ， - 2)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在 $\frac{22}{7}$ ， $\sqrt{5}$ ， $- \sqrt[3]{8}$ ， $π$ ，2023这五个数中无理数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 对于二元一次方程组 ${\begin{array}{l} y = x - 1 & ① \\ x - 2 y = 7 & ② \end{array}$ ，将①式代入②式，消去y可以得到（）

A、 $x - 2 x + 1 = 7$ B、 $x - 2 x - 2 = 7$ C、 $x + x + 1 = 7$ D、 $x - 2 x + 2 = 7$

查看试题解析
5. 一个容量为60的样本中，最大数是123，最小数是41，取组距为10，则可以分成（）

A、10组 B、9组 C、8组 D、7组

查看试题解析
6. 如图 $A D ⊥ B C$ 于点D， $A B = 6$ ， $A C = 9$ ， $A D = 5$ ，点P是线段BC上的一个动点，则线段AP的长度不可能是（）

A、5.5 B、7 C、8 D、4.5

查看试题解析
7. 番茄是我们常见的一种蔬菜，取5个大小均等的番茄放在同一简易天平秤，如图，则一个番茄的重量大约是（）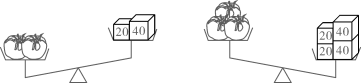

A、30 B、35 C、40 D、45

查看试题解析
8. 已知点Q的坐标为 $(2 ， - 3)$ ，点P的坐标为 $(2 a + 2 ， a - 5)$ ，若直线 $P Q ⊥ y$ 轴，则点P的坐标为（）

A、 $(2 ， - 5)$ B、 $(2 ， 2)$ C、 $(6 ， - 3)$ D、 $(- 14 ， - 3)$

查看试题解析
9. 已知，直线 $m ∥ n$ ，将一副三角板按如图所示的方式放置，直角顶点D在直线m上， $∠ F = 30 °$ ，另一直角三角板一直角边与直线n重合， $∠ C = 45 °$ ，若 $B C ∥ E F$ ，则 $∠ M D E =$ （）

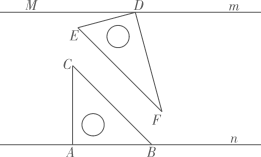A、10° B、15° C、20° D、30°

查看试题解析
10. 电影《刘三姐》中，有这样一个场景，罗秀才摇头晃脑地吟唱道：“三百条狗交给你，一少三多四下分，不要双数要单数，看你怎样分得匀?”该歌词表达的是一道数学题．其大意是：把300条狗分成4群，每个群里，狗的数量都是奇数，其中一个群，狗的数量少，另外三个群，狗的数量多且数量相同．问：应该如何分？刘三姐的姐妹们以对歌的形式给出答案：“九十九条打猎去，九十九条看羊来，九十九条守门口，剩下三条给财主．”刘三姐的姐妹们给出的答案是正确的，但不是唯一正确的答案．请算一算这个问题一共有多少种正确答案（）

A、12 B、24 C、50 D、99

查看试题解析

二、填空题（每小题3分，共15分）

11. 如图，利用工具测量角，得到 $∠ 1 = 30 °$ ，所使用的数学知识是．

查看试题解析
12. 比较大小： $\sqrt{7} - 2$ $\frac{1}{2}$ ．

查看试题解析
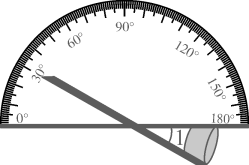13. 写出一个二元一次方程，使这个方程与 $x - y = 3$ 所组成的方程组的解为 ${\begin{cases} x = 2 \\ y = a \end{cases}$ ，这个方程可以是．

查看试题解析
14. 老李承包了村里两个鱼池，为了比较A、B两鱼池中鱼的数目，老李从两鱼池中各捞出200条鱼，每条做好记号，然后放回原鱼池．一段时间后，在同样的地方，老李再从A、B两鱼池中各捞出200条鱼，发现其中有记号的鱼分别是8条、15条，可以初步估计鱼数目较多的是鱼池．（填A或B）

查看试题解析
15. 新定义：对于实数x，我们规定 $[x]$ 表示不大于x的最大整数，例如 $[2.3] = 2$ ， $[3] = 3$ ， $[- 2.5] = - 3$ ，如果 $[x - 1] = - 2$ ，则实数x的取值范围是．

查看试题解析

三、解答题（共75分）

16.

(1)、计算： $\sqrt[3]{27} - | 3 - \sqrt{10} | - \sqrt{{(- 6)}^{2}}$

(2)、解不等式组： ${\begin{cases} 3 (x - 1) < x + 1 \\ \frac{x + 1}{2} - x \geq 1 \end{cases}$ ，请利用数轴求不等式组的解集．

查看试题解析
17. 已知 $7 a + 1$ 的立方根是 $\frac{1}{2}$ ， $8 a + b - 2$ 的平方根是 $\pm 2$ ．

(1)、求 $a$ ， $b$ 的值．

(2)、求 $- 8 a + 3 b + 3$ 的平方根．

查看试题解析
18. 已知 $x = 2$ ， $y = 4$ ； $x = 3$ ， $y = 1$ ；都是关于x，y的二元一次方程 $a x + b y = 10$ 的解．

(1)、求a，b的值；

(2)、当x为何值时，y的值小于0．

查看试题解析
19. 2023年“诗乡巩义·经典诵读”全民阅读暨“4·23”世界读书日活动启动以来，某校“综合与实践”活动小组为了解全校2700名学生的读书情况，随机抽取了若干名学生进行了调查，统计他们上一周末课外阅读时长t（单位：小时），并根据收集到的数据，整理后绘制了下列不完整的图表：

请你根据图表中提供的信息，解答下面的问题：

(1)、在调查活动中，该“综合与实践”活动小组调查方式是（填写“普查”或“抽样调查”）；

(2)、该“综合与实践”活动小组抽取的学生有人，扇形统计图中，4～6小时时间段对应扇形的圆心角的度数是；

(3)、请补全频数分布直方图；

(4)、请通过计算估计该校上一周学生周末课外阅读时长大于6小时的人数．

查看试题解析
20. 如图，已知BD平分 $∠ A B C$ ，过点A作 $A C ⊥ A B$ 交BC于点C，点D为角平分线BD上的一点，连接AD．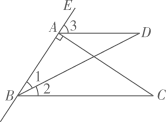

(1)、若 $∠ 3 + ∠ C = 90 °$ ，求证： $A D ∥ B C$ ．

(2)、在（1）的条件下， $∠ C = 28 °$ ，求 $∠ D$ 的度数．

查看试题解析
21. 如图，三角形ABC内任意一点 $P (x_{0} ， y_{0})$ ，经平移后对应点为 $P_{0} (x_{0} + 5 ， y_{0} - 5)$ ，将三角形ABC作同样的平移得到三角形 $A^{'} B^{'} C^{'}$ ，其中点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 分别为点A，B，C的对应点．

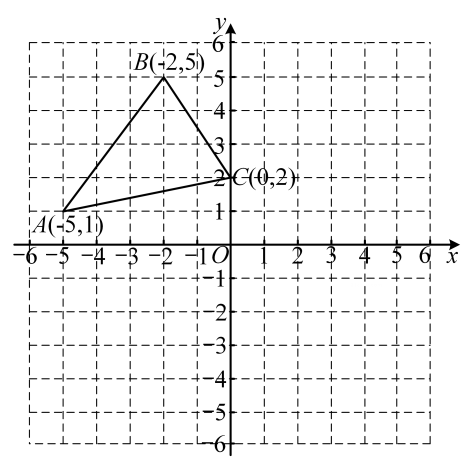(1)、请在所给的坐标系中画出三角形 $A^{'} B^{'} C^{'}$ ，并写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(2)、求四边形 $A A^{'} B^{'} B$ 的面积；

(3)、点D为y轴上一点，若三角形ACD的面积为三角形 $A^{'} C^{'} D$ 的面积的2倍，请直接写出点D的坐标．

查看试题解析
22. 端午节来临，李老师在超市购买了两种粽子礼盒．已知购买3盒红枣粽子与4盒蛋黄粽子所需款数相同；购买1盒红枣粽子和2盒蛋黄粽子共需100元．

(1)、求这两种粽子礼盒的单价；

(2)、李老师用不足300元购买了两种粽子礼盒共8盒，其中一盒红枣粽子内有10个，一盒蛋黄粽子内有6个，若他将粽子分给55名学生和10名任课教师，每人至少能拿到一个粽子，请根据以上信息，求李老师的购买方案及所花款数？

查看试题解析
23. 综合与实践
问题背景：
数学课上，同学们以“长方形纸带的折叠”为主题开展数学活动，已知长方形纸带的边 $A D ∥ B C$ ， $A B ∥ C D$ ， $∠ A = ∠ B = ∠ C = ∠ D = 90 °$ ，点 $B^{'}$ 为线段AD上一动点 $(A B^{'} \geq A B)$ ，将纸片折叠，使点B和点 $B^{'}$ 重合，产生折痕EF，点E是折痕与边AD的交点，点F是折痕与边BC的交点．

动手操作：

(1)、如图1，若点E与点A重合时，则 $∠ A F B$ 的度数为．
实践探究：

(2)、如图2，移动点 $B^{'}$ ，其余条件不变．
①小静发现图中无论点 $B^{'}$ 如何移动， $∠ A^{'} E B^{'} = ∠ B^{'} F C$ 始终成立，请说明理由；
②小东发现折叠后所形成的角，只要知道其中一个角的度数，就能求出其它任意一角的度数，若 $∠ A^{'} B^{'} E = 60 °$ ，求 $∠ B^{'} E F$ 的大小．

查看试题解析