2023年浙教版数学七年级上册5.1一元一次方程同步测试（提高版）

试卷更新日期：2023-10-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共24分）

1. 下列方程：
① $2 x^{2} - x = 6$ ；② $y = x - 7$ ；③ $\frac{2}{3} m - 5 = m$ ；④ $\frac{2}{x - 1} = 1$ ；⑤ $\frac{x - 3}{2} = 1$ ；⑥ $x = 3$ ，
其中是一元一次方程的有（）

A、2个 B、3个 C、4个 D、以上答案都不对

查看试题解析
2. 要使关于 $x$ 的方程 $3 (x - 2) + b = a (x - 1)$ 是一元一次方程，必须满足 $($ $)$

A、 $a \neq 0$ B、 $b \neq 0$ C、 $a \neq 3$ D、 $a$ 、 $b$ 为任意有理数

查看试题解析
3. 小明以每小时4千米的速度从家步行到学校上学，放学时以每小时3千米的速度按原路返回，结果发现比上学所花的时间多10分钟，如果设上学路上所花的时间为x小时，根据题意所列方程正确的是（）

A、 $4 x = 3 (x + \frac{1}{6})$ B、 $4 (x + \frac{1}{6}) = 3 x$ C、 $4 (x - \frac{1}{6}) = 3 x$ D、 $4 x = 3 (x - 10)$

查看试题解析
4. 两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的 $\frac{1}{3}$ ，这时增加了乙队，两队又共同工作了半个月，总工程全部完成，如果乙队单独完成总工程需多少个月？设乙队单独完成总工程共需 $x$ 个月，则下列方程正确的是（）

A、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{x} = 1$ B、 $\frac{1}{3} + \frac{1}{6} + \frac{1}{x} = 1$ C、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{2 x} = 1$ D、 $\frac{1}{3} + \frac{1}{2} (\frac{1}{3} + \frac{1}{x}) = 1$

查看试题解析
5. 某车间生产圆形铁片和长方形铁片，两个圆形铁片和一个长方形铁片可以制作成一个油桶（如图），已知该车间有工人42人，每个工人平均每小时可以生产圆形铁片120片或长方形铁片80片，为使生产的铁片恰好配套，设安排x人生产圆形铁片，可列方程（）

A、 $80 x = 2 \times 120 (42 - x)$ B、 $2 \times 80 x = 120 (42 - x)$ C、 $120 x = 2 \times 80 (42 - x)$ D、 $2 \times 120 x = 80 (42 - x)$

查看试题解析
6. “曹冲称象”是流传很广的故事，如图．按照他的方法：先将象牵到大船上，并在船侧面标记水位，再将象牵出．然后往船上抬入20块等重的条形石，并在船上留3个搬运工，这时水位恰好到达标记位置．如果再抬人1块同样的条形石，船上只留1个搬运工，水位也恰好到达标记位置．已知搬运工体重均为120斤，设每块条形石的重量是x斤，则正确的是（）

A、依题意3×120=x-120 B、依题意20x+3×120=(20+1)x+ 120 C、该象的重量是5040斤 D、每块条形石的重量是260斤

查看试题解析
7. 已知关于x的一元一次方程 $\frac{1}{2020} x + 3 = 2 x + b$ 的解为 $x = - 3$ ，那么关于y的一元一次方程 $\frac{1}{2020} (y + 1) + 3 = 2 (y + 1) + b$ 的解为（　　）

A、 $y = 1$ B、 $y = - 1$ C、 $y = - 3$ D、 $y = - 4$

查看试题解析
8. 小华在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是y- $\frac{1}{3}$ ＝ $\frac{1}{3}$ y-■，怎么办呢？小明想了想，便翻看了书后的答案，此方程的解是：y＝-6，小华很快补好了这个常数，并迅速完成了作业．这个常数是（）

A、-4 $\frac{2}{3}$ B、3 $\frac{2}{3}$ C、-4 $\frac{1}{3}$ D、4 $\frac{1}{3}$

查看试题解析

二、填空题（每题4分，共24分）

9. 在① $2 x - 1$ ；② $2 x + 1 = 3 x$ ；③ $| π - 3 | = π - 3$ ；④ $x + 1 = 3$ 中，等式有，方程有．（填入式子的序号）

查看试题解析
10. 如图，小红同学编了一道数学谜题，若设“□”内的数字为x，则可列出方程为.

查看试题解析
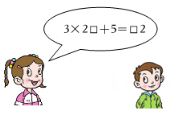11. 写出一个方程，使其满足下列条件：
⑴它是关于 $x$ 的一元一次方程；
⑵该方程的解为 $x = 3$ ；
⑶在求解过程中，至少运用一次等式基本性质进行变形；
则该方程可以是 $($ 写出一个满足条件的方程即可 $)$ ．

查看试题解析
12. 在等式- $\frac{3}{x + 1}$ ＝1、x＝0、 $\frac{x}{π}$ +1＝4-2x、x-2y＝ $\frac{1}{2}$ 、2x²-2x＝ $\frac{1}{2}$ 中，一元一次方程的个数为.

查看试题解析
13. 《孙子算经》中有一道题，原文是：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车；若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有x人，可列方程．

查看试题解析
14. 若3x^2m-3+9=1是关于x的一元一次方程，则m的值为

查看试题解析
15. 关于 $x$ 的方程 $3 x + 2 m = 9$ 的解是 $x = 1$ ，则 $m$ 的值是.

查看试题解析

三、解答题（共9题，共72分）

16. 判断下列各式是不是方程，不是的说明为什么

(1)、4×5=3×7﹣1

(2)、2x+5y=3．

(3)、9﹣4x＞0．

(4)、 $\frac{x - 3}{2} = \frac{1}{3}$

(5)、2x+3．

查看试题解析
17. 在初中数学中，我们学习了各种各样的方程．以下给出了6个方程，请你把属于一元方程的序号填入圆圈（1）中，属于一次方程的序号填入圆圈（2）中，既属于一元方程又属于一次方程的序号填入两个圆圈的公共部分．
①3x+5=9：②x²+4x+4=0；③2x+3y=5：④x²+y=0；⑤x﹣y+z=8：⑥xy=﹣1．

查看试题解析
18. 已知方程（3m﹣4）x²﹣（5﹣3m）x﹣4m=﹣2m是关于x的一元一次方程，
（1）求m和x的值．
（2）若n满足关系式|2n+m|=1，求n的值．

查看试题解析
19. 已知（a﹣2）x²+ax+1=0是关于x的一元一次方程（即x是未知数），求这个方程的解．

查看试题解析
20. 根据题意列出方程．

(1)、一个数的 $\frac{1}{7}$ 与3的差等于最大的一位数，求这个数；

(2)、从正方形的铁皮上，截去2 cm宽的一个长方形条，余下的面积是80 cm² ，那么原来的正方形铁皮的边长是多少？

(3)、某商店规定，购买超过15 000元的物品可以采用分期付款方式付款，顾客可以先付3 000元，以后每月付1 500元．王叔叔想用分期付款的方式购买价值19 500元的电脑，他需要用多长时间才能付清全部货款？

查看试题解析
21. 把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个长为 $m$ ，宽为 $n$ 的长方形内，该长方形内部未被卡片覆盖的部分用阴影表示.

(1)、能否用只含 $n$ 的式子表示出图②中两块阴影部分的周长和？（填“能”或“不能”）；

(2)、若能，请你用只含 $n$ 的式子表示出中两块阴影部分的周长和；若不能，请说明理由.

查看试题解析
22. 某自来水公司按如下规定收取水费：每月用水不超过10吨，按每吨1.5元收费；每月用水超过10吨，超过部分按每吨2元收费．设每月用水量为x吨．

(1)、小红家3月用水10吨，应交水费多少元？

(2)、试用x的代数式表示付水费的费用．

(3)、小明家4月份的水费是25元，小明家4月份用水多少吨？

查看试题解析
23. 已知代数式 $M = 3 (a - 2 b) - (b + 2 a)$ .

(1)、化简 $M$ ；

(2)、如果 $(a + 2) x^{2} + 4 x^{b - 2} - 3 = 0$ 是关于 $x$ 的一元一次方程，求 $M$ 的值.

查看试题解析
24. 关于 $x$ 的方程 $(m - 1) x^{n} - 3 = 0$ 是一元一次方程．

(1)、则m，n应满足的条件为：m ， n；

(2)、若此方程的根为整数，求整数m的值．

查看试题解析

2023年浙教版数学七年级上册5.1一元一次方程 同步测试（提高版）

一、选择题（每题3分，共24分）

二、填空题（每题4分，共24分）

三、解答题（共9题，共72分）

2023年浙教版数学七年级上册5.1一元一次方程同步测试（提高版）