2023年浙教版数学七年级上册5.1一元一次方程同步测试（培优版）

试卷更新日期：2023-10-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列各式中：① $2 x - 1 = 5$ ；② $4 + 8 = 12$ ；③ $5 y + 8$ ；④ $2 x + 3 y = 0$ ；⑤ $2 a + 1 = 1$ ；⑥ $2 x^{2} - 5 x - 1$ ，是方程的是（）

A、①④ B、①②⑤ C、①④⑤ D、①②④⑤

查看试题解析
2. 根据下面所给条件，能列出方程的是（）

A、一个数的 $\frac{1}{3}$ 是6 B、x与1的差的 $\frac{1}{4}$ C、甲数的2倍与乙数的 $\frac{1}{3}$ D、a与b的和的60%

查看试题解析
3. 对于等式： $| x - 1 | + 2 = 3$ ，下列说法正确的是（）

A、不是方程 B、是方程，其解只有2 C、是方程，其解只有0 D、是方程，其解有0和2

查看试题解析
4. 下列各式中，是一元一次方程的有（）
（1） $x + π > 3$ ；（2） $12 - x$ ；（3） $2 + 3 = 5 x$ ；（4） $x - y = 3$ ；（5） $t = 1$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡有x只，可列方程为（）

A、 $4 x + 2 (94 - x) = 35$ B、 $4 x + 2 (35 - x) = 94$ C、 $2 x + 4 (94 - x) = 35$ D、 $2 x + 4 (35 - x) = 94$

查看试题解析
6. 按如图所示的运算程序：若输入x的值是29，则输出结果是（　　）

A、257 B、261 C、286 D、293

查看试题解析
7. 元朝朱世杰所著的《算学启蒙》中，记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？其大意是：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马？若设快马 $x$ 天可追上慢马，由题意得（）

A、 $\frac{x}{240} = \frac{x + 12}{150}$ B、 $\frac{x}{240} = \frac{x}{150} - 12$ C、 $240 (x - 12) = 150 x$ D、 $240 x = 150 (x + 12)$

查看试题解析
8. 2020年11月1日零时，我国开展第七次全国人口普查.2021年5月11日，国务院新闻办公室公布普查结果，如图是根据我国历次人口普查数据，绘制的我国每10万人中拥有大学文化(指大专及以上)程度人数的折线图.设2020年每10万人中拥有大学文化程度的人数与2010年相比的增长率为x，则下列关于x的方程正确的是 (　　)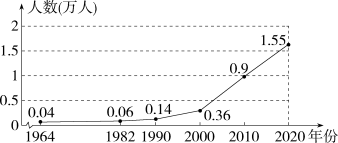

A、(1+0.9)x=1.55　　　　 B、0.9(1+x)×10=1.55 C、0.9(1+x)=1.55　　　　 D、0.9(1+x)¹⁰=1.55

查看试题解析
9. 已知方程 $(m - 2) x^{| m | - 1} + 7 = 0$ 是关于x的一元一次方程，则 $m =$ （　　）

A、2 B、 $\pm 1$ C、 $- 2$ D、 $\pm 2$

查看试题解析
10. 方程 $- 3 (★ - 9) = 5 x - 1$ ， ★处被盖住了一个数字，已知方程的解是 $x = 2$ ，那么★处的数字是（）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题（每题4分，共24分）

11. 观察方程 $x^{5} － 2 x － y = 0$ ， $2 x^{4} y + 3 x^{2} + 1 = 0$ ， $x^{5} － 2 x^{4} y + 2 y^{5} = 0$ ， $4 x^{5} － 4 x y = 0$ 的未知数的个数和未知数的次数，从这些方程的共同特征，可以将它们称为．

查看试题解析
12. 《九章算术》是中国古代一部重要的数学典籍，被视为“算经之首”．其中有这样一个问题：今有共买金，人出四百，盈三千四百；人出三百，盈三百．问人数，金价各几何？其大意是，假设合伙买金，每人出400钱，还剩余3400钱；每人出300钱，还剩余300钱．问人数，金价各是多少？如果设有x个人，根据题意所列方程为．

查看试题解析
13. 《莱因德纸草书》是古埃及培训年轻抄写员时可能使用的问题合集，其中记载了下列一个简单的问题：一个量与它的一半及它的三分之一加在一起变成10.若设这个量为x，则根据题意可列出方程.

查看试题解析
14. 若方程 $(k + 2) x^{| k + 1 |} + 6 = 0$ 是关于 $x$ 的一元一次方程，则 $k + 2023 =$ ．

查看试题解析
15. 若关于x的一元一次方程 $x - m + 4 = 0$ 的解是负数，则m的取值范围是．

查看试题解析
16. 已知关于x的方程 $3 a - x = x + 2$ 的解为 $x = 2$ ，则代数式 $a^{2} - 2 a + 1$ 的值是．

查看试题解析

三、解答题（共8题，共66分）

17. 某校七年级的一名学生做作业时，不慎将墨水瓶打翻，使一道题只看到如下字样：“甲、乙两地相距120千米”，摩托车的速度为45千米/时，运货汽车的速度为35千米/时，？请你将这道题补充完整，并列出方程．

查看试题解析
18. 根据下列题干设未知数列方程，并判断它是不是一元一次方程．

(1)、从60cm的木条上截去2段同样长的木棒，还剩下10cm长的短木条，截下的每段为多少？

(2)、小红对小敏说：“我是6月份出生的，我的年龄的2倍加上10，结果正好是我出生的那个月的总天数，你猜我有几岁？”

查看试题解析
19. 已知方程(3m-4)x²-(5-3m)x-4m=-2m是关于x的一元一次方程.

(1)、求m和x的值.

(2)、若n满足关系式|2n+m|=1，求n的值.

查看试题解析
20. 已知方程（1﹣m²）x²﹣（m+1）x+8＝0是关于x的一元一次方程.

(1)、求m的值及方程的解.

(2)、求代数式 $5 x^{2} - 2 (x m + 2 x^{2}) - 3 (\frac{1}{3} x m + 2)$ 的值.

查看试题解析
21. 已知方程 $(1 - m^{2}) x^{2} - (m + 1) x + 8 = 0$ 是关于x的一元一次方程.

(1)、求代数式 $5 x^{2} - 2 (x m + 2 x^{2}) - 3 (\frac{1}{3} x m + 2)$ 的值；

(2)、求关于y的方程 $m | y + 2 | = x$ 的解.

查看试题解析
22. 已知 $(m - 3) x^{| m | - 2} + 6 = 0$ 是关于x的一元一次方程.

(1)、求m的值；

(2)、若 $| y - m | = 3$ ，求出y的值；

(3)、若数a满足 $| a | \leq | m |$ ，试化简： $| a + m | + | a - m |$ .

查看试题解析
23. 学校计划购买6张“双鱼”牌乒乓球桌和a副“红双喜”牌乒乓球拍（不少于6副）． A、B两家体育商品店的价格相同，球桌每张1000元，球拍每副200元．A店优惠政策是每买一张乒乓球桌，送一副球拍；B店的优惠政策为所有商品打八五折．

(1)、规定只能到其中一个店购买乒乓球桌和乒乓球拍，请分别用含a的代数式表示在A、B两家体育商品店购买这些物品所需的费用，并化简．

(2)、若到A、B两家店购买，所需费用相等，求a的值．

查看试题解析
24. 我们规定，若关于x的一元一次方程ax=b的解为x=b-a，则称该方程为“定值方程”.例如：2x=4的解为x=2=4-2，则该方程2x=4是“定值方程”.请根据上述规定解答下列问题：

(1)、判断方程4x=6 （回答“是”或“不是”）“定值方程”；

(2)、若a=3，有符合要求的“定值方程”吗？若有，求b的值；若没有，请说明理由.

(3)、若关于x的一元一次方程2x=mn+m和-2x=mn+n都是“定值方程”，求代数式5-3m+3n的值.

查看试题解析

2023年浙教版数学七年级上册5.1一元一次方程 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学七年级上册5.1一元一次方程同步测试（培优版）