(人教版)2023-2024学年八年级数学上册 12.2 三角形全等的判定 期中专项复习
试卷更新日期:2023-10-10 类型:复习试卷
一、选择题
-
1. 如图,已知 , , 那么添加下列一个条件后,能判定≌的是( )
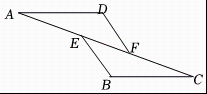 A、 B、 C、 D、2. 如图,点、、、在一条直线上, , , 下列条件中,能判断的是( )
A、 B、 C、 D、2. 如图,点、、、在一条直线上, , , 下列条件中,能判断的是( )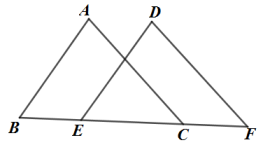 A、 B、 C、 D、3. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角4. 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A、 B、 C、 D、3. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角4. 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )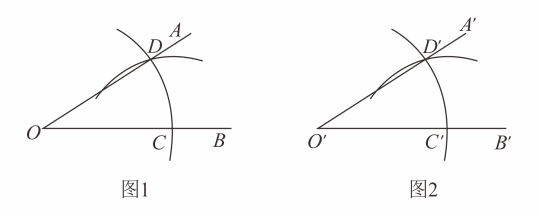 A、SAS B、ASA C、AAS D、SSS5. 如图,在和中,点、、、在同一条直线上, , , 只添加一个条件,不能判断≌的是( )
A、SAS B、ASA C、AAS D、SSS5. 如图,在和中,点、、、在同一条直线上, , , 只添加一个条件,不能判断≌的是( ) A、 B、 C、 D、6. 如图,的顶点在的边上,且 , , , 则下列说法不正确的是( )
A、 B、 C、 D、6. 如图,的顶点在的边上,且 , , , 则下列说法不正确的是( ) A、≌ B、 C、 D、7. 如图,点A , E , F , D在同一直线上,若 , , , 则图中的全等三角形共有( )
A、≌ B、 C、 D、7. 如图,点A , E , F , D在同一直线上,若 , , , 则图中的全等三角形共有( ) A、0对 B、1对 C、2对 D、3对8. 如图, , , 与相交于点 , 过点并分别交 , 于点 , , 则图中的全等三角形共有( )
A、0对 B、1对 C、2对 D、3对8. 如图, , , 与相交于点 , 过点并分别交 , 于点 , , 则图中的全等三角形共有( ) A、对 B、对 C、对 D、对9. 如图,已知 , 欲用“边角边”证明≌ , 需补充条件( )
A、对 B、对 C、对 D、对9. 如图,已知 , 欲用“边角边”证明≌ , 需补充条件( ) A、 B、 C、 D、10. 如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( )
A、 B、 C、 D、10. 如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 如图,在 中, , , ,射线 于点A,点E、D分别在线段 和射线 上运动,并始终保持 ,要使 和 全等,则 的长为.
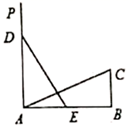 12. 如图,点 , , , 在同一条直线上, , , 若 , , 则的度数为
12. 如图,点 , , , 在同一条直线上, , , 若 , , 则的度数为 13. 如图,于于 , 且点从向运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发运分钟后,与全等.
13. 如图,于于 , 且点从向运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发运分钟后,与全等. 14. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
14. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 15. 如图,在中,为中点,为边上的动点,连接 , 交的延长线于点 , 若 , 则的值是.
15. 如图,在中,为中点,为边上的动点,连接 , 交的延长线于点 , 若 , 则的值是.
三、解答题
-
16. 如图, , , , 求证 .
 17. 如图,已知 , , , 与交于点 .
17. 如图,已知 , , , 与交于点 . (1)、求证:≌;(2)、若 , 求的度数.18. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)、求证:≌;(2)、若 , 求的度数.18. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.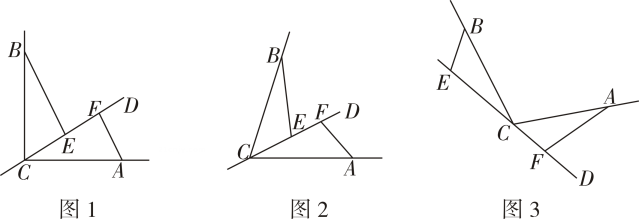 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.
(2)、如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF、BE,AF三条线段数量关系的合理猜想,并简述理由.19. 如图,中,是边上的中线, , 为直线上的点,连接 , , 且 .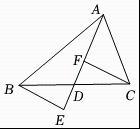 (1)、求证:≌;(2)、若 , , 试求的长.
(1)、求证:≌;(2)、若 , , 试求的长.四、综合题
-
20. 如图 , 在平面直角坐标系中,点 , 连接 , 将绕点逆时针方向旋转到 .
 (1)、求点的坐标;用字母 , 表示(2)、如图 , 延长交轴于点 , 过点作交轴于点 , 求证: .
(1)、求点的坐标;用字母 , 表示(2)、如图 , 延长交轴于点 , 过点作交轴于点 , 求证: .


