(人教版)2023-2024学年八年级数学上册 12.1 全等三角形 期中专项复习
试卷更新日期:2023-10-10 类型:复习试卷
一、选择题
-
1. 如图,图中的两个三角形全等,则∠α等于( )
 A、71° B、59° C、58° D、50°2. 如图,点 , , , 在同一条直线上, , , 则添加下列条件中的一个条件后,不一定能判定≌的是( )
A、71° B、59° C、58° D、50°2. 如图,点 , , , 在同一条直线上, , , 则添加下列条件中的一个条件后,不一定能判定≌的是( )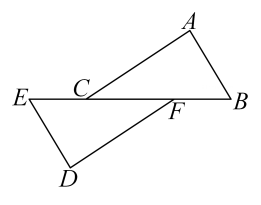 A、 B、 C、 D、3. 如图,已知 , , , 则的长为( )
A、 B、 C、 D、3. 如图,已知 , , , 则的长为( ) A、7 B、3.5 C、3 D、24. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )
A、7 B、3.5 C、3 D、24. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )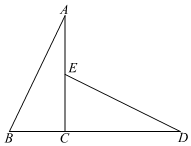 A、1.5 B、2 C、4.5 D、65. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A、1.5 B、2 C、4.5 D、65. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( ) A、12 B、7 C、2 D、146. 下列四个图形中,属于全等图形的是( )
A、12 B、7 C、2 D、146. 下列四个图形中,属于全等图形的是( )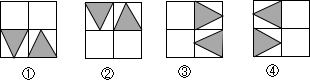 A、①和② B、②和③ C、①和③ D、③和④7. 如图,点A,E,C在同一直线上, , , , 则BC的长为( )
A、①和② B、②和③ C、①和③ D、③和④7. 如图,点A,E,C在同一直线上, , , , 则BC的长为( ) A、3 B、5 C、8 D、118. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( )
A、3 B、5 C、8 D、118. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( ) A、 B、 C、 D、9. 如图, , 过点作 , 垂足为 , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图, , 过点作 , 垂足为 , 若 , 则的度数为( )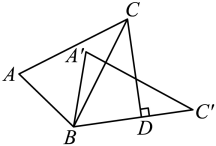 A、 B、 C、 D、10. 如图,若 , 则等于( )
A、 B、 C、 D、10. 如图,若 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,、、在同一直线上,≌ , , 那么度.
 12. 如图,已知≌ , , 则 度.
12. 如图,已知≌ , , 则 度. 13. 如图,若△ABC≌△DEF , AF=2,FD=8,则FC的长度是 .
13. 如图,若△ABC≌△DEF , AF=2,FD=8,则FC的长度是 . 14. 一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5, , , 若这两个三角形全等,则的值是 .15. 如图,在平面直角坐标系中,点 , 的坐标分别是 , , , 若点在轴的正半轴上,则位于第四象限的点的坐标是 .
14. 一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5, , , 若这两个三角形全等,则的值是 .15. 如图,在平面直角坐标系中,点 , 的坐标分别是 , , , 若点在轴的正半轴上,则位于第四象限的点的坐标是 .
三、解答题
-
16. 下面是教材中“作一个角等于已知角”的尺规作图过程已知: , 求作:一个角 , 使它等于 .
作法:如图,作射线;
以为圆心,任意长为半径作弧,交于 , 交于;
以为圆心,为半径作弧 , 交于;
以为圆心,为半径作弧,交弧于;
过点作射线 , 则就是所求作的角.
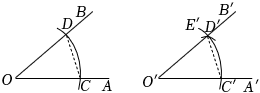
请完成下列问题:
(1)、该作图的依据是 填序号 .(2)、请证明 .17. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数. 18. 如图,△ABE≌△DCE,点A,C,B在一条直线上,∠AED和∠BEC相等吗?为什么?
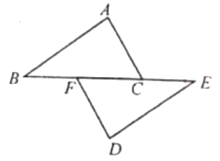
18. 如图,△ABE≌△DCE,点A,C,B在一条直线上,∠AED和∠BEC相等吗?为什么? 19. 如图,点B、F、C,E在同一直线上,BF=CE,AB∥ED,AC∥FD.
19. 如图,点B、F、C,E在同一直线上,BF=CE,AB∥ED,AC∥FD.求证:AB=DE.
四、综合题
-
20. 如图所示,已知△ABD≌△CFD,AD⊥BC于D.
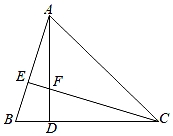 (1)、求证:CE⊥AB;(2)、已知BC=7,AD=5,求AF的长.21. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,BF平分∠ABC交AC于点F,AE⊥BF于点E,AE,BC的延长线交于点M.
(1)、求证:CE⊥AB;(2)、已知BC=7,AD=5,求AF的长.21. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,BF平分∠ABC交AC于点F,AE⊥BF于点E,AE,BC的延长线交于点M. (1)、求证:AB=BM;(2)、求证:BF=2AE.
(1)、求证:AB=BM;(2)、求证:BF=2AE.

