（人教版）2023-2024学年八年级数学上册 11.3 多边形及其内角和 期中专项复习
试卷更新日期：2023-10-10 类型：复习试卷
一、选择题
-
1. 如图，要使一个七边形木架不变形，至少要再钉上木条的根数是（ ）
A、1根 B、2根 C、3根 D、4根2. 若从边形的一个顶点出发，可以画出条对角线，则的值是（ ）A、 B、 C、 D、3. 一个正多边形的每一个内角是 ，则从这个正多边形的一个顶点出发可作（ ）条对角线．A、5 B、4 C、3 D、24. 过m边形的一个顶点有12条对角线，n边形没有对角线，则 的值为（ ）A、27 B、30 C、36 D、455. 从一个多边形的一个顶点出发共可作10条对角线，则这个多边形共有对角线的条数为（ ）A、35 B、65 C、70 D、1306. 如果一个多边形的内角和是它的外角和的2倍，那么从这个多边形的边数是（ ）A、5 B、6 C、4 D、77. 如图，（ ）
A、480 B、500° C、540° D、600°8. 一个多边形截取一个角后，形成另一个多边形的内角和是1620，则原来多边形的边数是（ ）A、10 B、11 C、12 D、以上都有可能9. 一块多边形木板截去一个三角形后截线不经过顶点 ， 得到的新多边形的内角和为 ， 则原多边形的边数为（ ）A、 B、 C、 D、10. 以下关于多边形内角和与外角和的表述，错误的是（ ）A、四边形的内角和与外角和相等 B、如果一个四边形的一组对角互补，那么另一组对角也互补 C、六边形的内角和是外角和是2倍 D、如果一个多边形的每个内角是120°，那么它是十边形．二、填空题
-
11. 正边形的每个内角都是 ， 这个正边形的对角线条数为条．12. 一个凸 边形的边数与对角线条数的和小于20，且能被5整除，则 ．13. 若从一个多边形一个顶点出发，最多可以引12条对角线，则它的边数为 ．14. 如图所示， ．
15. 如图，小陈从点出发，前进米后向右转 ， 再前进米后又向右转 ， ， 这样一直走下去，他第一次回到出发点时一共走了米．
三、解答题
-
16. 已知一个多边形的内角和比外角和的倍多 ， 则这个多边形的边数是多少？17. 已知在一个十边形中，其中九个内角的和是 ， 求这个十边形另一个内角的度数．18. 已知从m边形的一个顶点出发可以画4条对角线；从n边形的一个顶点出发的所有对角线把n边形分成6个三角形．求的值．19. 已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍，求此多边形的边数．
四、综合题
-
20. 已知一个正多边形共有35条对角线，求：(1)、这个正多边形的边数(2)、这个正多边形每个内角和每个外角的度数21.
求解：根据问题回答：
(1)、如图（1），O为四边形ABCD内一点，连接OA、OB、OC、OC可以得几个三角形？它与边数有何关系？(2)、如图（2），O在五边形ABCDE的AB上，连接OC、OD、OE，可以得到几个三角形？它与边数有何关系？(3)、如图（3），过A作六边形ABCDEF的对角线，可以得到几个三角形？它与边数有何关系？22. 如图，在四边形中， ， 分别是及的平分线.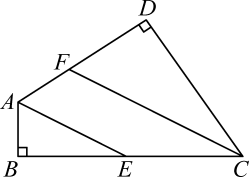
(1)、求证：；(2)、若 ， 求.23. 在△ABC中，∠A＝70°，点D、E分别是边AC、AB上的点（不与A、B、C重合）点P是平面内一动点（P与D、B不在同一直线上），设∠PEB＝∠1，∠DPE＝∠2，∠PDC＝∠3．
(1)、若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠2＝；（用含有∠1、∠3的代数式表示）(2)、若点P在△ABC的外部，如图（2）所示，则∠1、∠2、∠3之间有何关系？写出你的结论，并说明理由．(3)、当点P在边CB的延长线上运动时，试画出相应图形，标注有关字母与数字，直接写出对应的∠1、∠2、∠3之间的关系式．