(人教版)2023-2024学年八年级数学上册 11.2 与三角形有关的角 期中专项复习
试卷更新日期:2023-10-10 类型:复习试卷
一、选择题
-
1. 如图,将一块三角尺的直角顶点放在直线a上,a∥b , 则∠2=( )
 A、80° B、70° C、60° D、50°2. 如图,在中, , , 是的平分线,则的大小为( )
A、80° B、70° C、60° D、50°2. 如图,在中, , , 是的平分线,则的大小为( ) A、
A、
B、
C、
D、3. 如图,点是内一点, , , , 则( ) A、 B、 C、 D、4. 在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A、40° B、45° C、50° D、60°5. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°6. 如图,已知 , , ,则 的度数为( )
A、 B、 C、 D、4. 在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A、40° B、45° C、50° D、60°5. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°6. 如图,已知 , , ,则 的度数为( )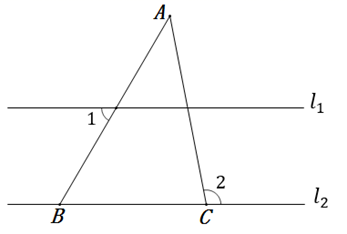 A、50° B、55° C、45° D、60°7. 在中,分别是高和角平分线,点F在的延长线上,交于点G , 交于点H , 下列结论:
A、50° B、55° C、45° D、60°7. 在中,分别是高和角平分线,点F在的延长线上,交于点G , 交于点H , 下列结论:①;
②;
③ ,
④;
其中正确的有( )个.
 A、1 B、2 C、3 D、48. 如图,是的平分线, , , 则( )
A、1 B、2 C、3 D、48. 如图,是的平分线, , , 则( ) A、 B、 C、 D、9. 如图,若 , , , 则等于( )
A、 B、 C、 D、9. 如图,若 , , , 则等于( ) A、 B、 C、 D、10. 把一副三角板按如图所示摆放,使 , 点恰好落在的延长线上,则的大小为 ( )
A、 B、 C、 D、10. 把一副三角板按如图所示摆放,使 , 点恰好落在的延长线上,则的大小为 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , , , 平分则的度数为 .
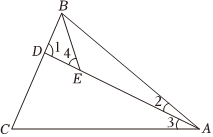 12. 如图,中, , 边上有一点 , 使得 , 将沿翻折得 , 此时 , 则度.
12. 如图,中, , 边上有一点 , 使得 , 将沿翻折得 , 此时 , 则度. 13. 空竹是我国传统的一项游戏,其器材简单但是动作花样繁多,深受大众喜爱彤彤在跑步时发现广场上抖空竹的老奶奶的某个动作可以抽象成一个简单的数学图形,如图所示, , , , 则的度数是 .
13. 空竹是我国传统的一项游戏,其器材简单但是动作花样繁多,深受大众喜爱彤彤在跑步时发现广场上抖空竹的老奶奶的某个动作可以抽象成一个简单的数学图形,如图所示, , , , 则的度数是 . 14. 如图, , , 则的度数为 .
14. 如图, , , 则的度数为 . 15. 如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2=度.
15. 如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2=度.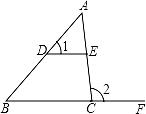
三、解答题
-
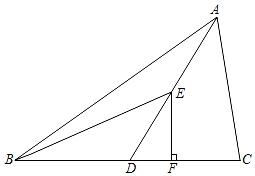
16. 如图,中,是的中线,是的角平分线,是的高.
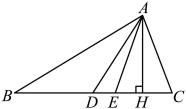 (1)、若的面积为8, , 求的长;(2)、若 , 求的度数.17. 如图,已知D是上一点,E是上的一点,、相交于点F , , , .
(1)、若的面积为8, , 求的长;(2)、若 , 求的度数.17. 如图,已知D是上一点,E是上的一点,、相交于点F , , , . (1)、的度数;(2)、的度数.18. 如图,已知三角形ABC的三个内角平分线交于点I , 于H , 试比较∠CIH和∠BID的大小.
(1)、的度数;(2)、的度数.18. 如图,已知三角形ABC的三个内角平分线交于点I , 于H , 试比较∠CIH和∠BID的大小. 19. 如图,四边形ABCD中,AE , DF分别是∠BAD , ∠ADC的平分线,且于点O . 延长DF交AB的延长线于点M .
19. 如图,四边形ABCD中,AE , DF分别是∠BAD , ∠ADC的平分线,且于点O . 延长DF交AB的延长线于点M . (1)、求证:;(2)、若 , , 求∠C , ∠DFE的度数.
(1)、求证:;(2)、若 , , 求∠C , ∠DFE的度数.四、综合题
-
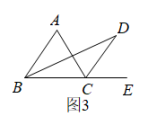
20. 如图,AE平分∠BAC,∠CAE=∠CEA.
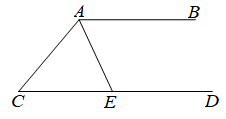 (1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图
(1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图 (1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
(1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.