【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练:第13题
试卷更新日期:2023-10-09 类型:二轮复习
一、原题
-
1. 已知向量 , 满足
二、基础
-
2. 已知平面向量 , , 与的夹角为 , 则 .3. 设向量 , 为单位正交基底,若 , , 且 , 则.4. 已知外接圆的圆心为是边上一动点,若 , 则的最大值为.5. 已知向量 , 的夹角为 , , 则在方向上的数量投影为.6. 已知向量 , 满足 , , 则.7. 正六边形的边长为4,点满足 , 则.8. 在平行四边形中, , , , 则.9. 设向量、满足 , , 则.10. 若向量、满足 , , 则.11. 是边长为1的等边三角形,点M为边AB的中点,则 .12. 已知夹角为的非零向量满足 , , 则.
三、提升
-
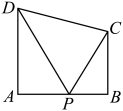
13. 四边形中,点分别是的中点, , 点满足 , 则的最大值为 .14. 如果平面向量 , 那么向量在上的投影向量为.15. 已知向量 , 满足 , , 且 , 则;向量与的夹角的余弦值为16. 已知平面向量 , , 均为非零向量, , 且 , , 则的最小值为.17. 已知正方形的边长为4,若 , 则的值为.18. 已知等边的重心为O,边长为3,则.19. 如图.在直角梯形中. , 点P是腰上的动点,则的最小值为 .
 20. 已知单位向量 , 的夹角为60°,若 , 则记作 . 已知向量 , , 则 .21. 已知抛物线:的焦点为 , 经过抛物线上一点 , 作斜率为的直线交的准线于点 , 为准线上异于的一点,当时, .22. 已知非零向量 , , 满足 , , 的夹角为120°,且 , 则向量 , 的数量积为 .23. 如图,矩形中, , , 为的中点. 当点在边上时,的值为;当点沿着 , 与边运动时,的最小值为.
20. 已知单位向量 , 的夹角为60°,若 , 则记作 . 已知向量 , , 则 .21. 已知抛物线:的焦点为 , 经过抛物线上一点 , 作斜率为的直线交的准线于点 , 为准线上异于的一点,当时, .22. 已知非零向量 , , 满足 , , 的夹角为120°,且 , 则向量 , 的数量积为 .23. 如图,矩形中, , , 为的中点. 当点在边上时,的值为;当点沿着 , 与边运动时,的最小值为.
四、培优
-
24. 已知平面向量、、、、、两两互不相等,且.若对任意的 , 均满足 , 则当且时,的值为.25. 已知向量 , 的夹角为 , 且 , 向量满足 , 且 , 记 , , 则的最大值为.
-