吉林省长春市2023年中考数学四模试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. 实数﹣2的倒数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 成都作为中国西部大开发的重要战略支点，是立足“一带一路”建设和长江经济发展的重要节点，充分发挥服务国家向西向南开放的独特区位优势， 2022年实现外贸进出口达8300亿元，将数据“8300亿”用科学记数法表示应为（　　）

A、8.3×10¹¹ B、8.3×10¹⁰ C、83×10⁹ D、0.83×10⁸

查看试题解析
3. 下列计算正确的是（　　）

A、a²+a⁴＝a⁶ B、 ${(\frac{a}{b})}^{4} = \frac{a^{4}}{b^{4}}$ C、（-a²）³＝a⁶ D、（a-b）（b+a）＝b²-a²

查看试题解析
4. 下列四个几何体中，三视图中不含矩形的是（　　）

A、 B、 C、 D、

查看试题解析
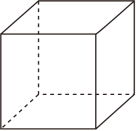5. 静乐一兴县高速公路（简称静兴高速）通车后，大大方便了人们的出行．据了解从兴县到太原的车程为202公里，汽车平均车速提高为原来的1.6倍，从兴县到太原所用时间比原来节省了1.8小时，设从兴县到太原原来所用时间为x小时，根据题意可列方程为（　　）

A、 $\frac{202}{x} = \frac{202}{1.6 x} + 1.8$ B、 $\frac{202}{x} \times 1.6 = \frac{202}{x - 1.8}$ C、 $\frac{202}{x} = \frac{202}{1.6 x} - 1.8$ D、 $\frac{202}{x} \times 1.6 = \frac{202}{x + 1.8}$

查看试题解析
6. 如图，在△ABC中，∠A＝88°，∠B＝50°，AB＝60，则点A到BC的距离为（　　）

A、60sin50° B、 $\frac{60}{s i n 5 0^{°}}$ C、60cos50° D、60tan50°

查看试题解析
7. 如图，在△ABC中，∠ACB＝90°， ∠A=39° ，以点C为圆心，CB长为半径作弧交AB于点D，B为圆心，大于 $\frac{1}{2} D B$ ，两弧相交于点E，作射线CE交AB于点F，求∠BCF的度数（　　）

A、38° B、39° C、40° D、51°

查看试题解析
8. 如图，已知正方形ABCD的面积为4，它的两个顶点B和D在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 图像上，若点D的坐标是（a，b），求a-b的值，（　　）

A、 $\frac{1}{2}$ B、 $- \frac{3}{4}$ C、2 D、-2

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

9. 分解因式：mn-9m＝．

查看试题解析
10. 若分式 $\frac{- 6}{7 - x}$ 的值为正数，则x的取值范围．

查看试题解析
11. 将一副三角板按如图所示放置，则∠1的度数为．

查看试题解析
12. 如图，以点O为位似中心，作△ABC的位似图形△A'B'C'．已知 $\frac{O A}{O A^{^{'}}} = \frac{1}{3}$ ，若△ABC的面积是3，则△A´B´C´的面积为．

查看试题解析

13. 某工厂生产电子芯片，质检部门对同一批产品进行随机抽样检测，检测结果统计如表：由此估计这批产品合格的概率为．（精确到0.01）

抽查数n	1000	2000	3000	4000	5000
合格品数m	957	1926	2868	3844	4810
合格品频率 $\frac{m}{n}$	0.957	0.963	0.956	0.961	0.962

查看试题解析

14. 二次函数y＝（x-h）²+k（h、k均为常数）的图象经过P₁（-3，y₁）、P₂（-1，y₂）、P₃（1，y₃）三点．若y₂＜y₁＜y₃ ，则h的取值范围是．

查看试题解析

三、解答题（本大题共10个小题，共78分）

15. 先化简，再求值：（x+1）²-x（x+1），其中x＝2023．

查看试题解析
16. 动力电池常常应用于电动汽车、电动船、电动列车和电动自行车等交通工具．为拓宽学生科技视野，某校开展科普知识进校园活动．九年级（1）班选出小致为全校同学介绍应用动力电池的两种交通工具（图片除编号和内容外，其余完全相同）．将这四张图片背面朝上，洗匀放好（不放回），再从中随机抽取一张，请用列表或画树状图的方法求他抽到的两张图片编号恰好是A和D的概率．

查看试题解析
17. 太原的王先生积极响应国家有关政策，在某社区投资建成了一个养老服务中心和一个老年食堂，总面积为500平方米．太原市政府出台社会力量参与社区和居家养老可享受优惠政策：建设社区养老服务中心可获得700元/平方米的补贴，老年食堂可获得1400元/平方米的补贴，两种补贴一共获得490000元，求王先生投资的养老服务中心和老年食堂的面积分别为多少平方米．

查看试题解析
18. 如图，四边形OACB的顶点A，B，C在以点O为圆心的同一个圆上，点C是 $\overset{⌢}{A B}$ 的中点，连接OC并延长交圆O的切线BD于点D ，过点B作 $⊙$ O的切线交OC的延长线于点D，已知∠D＝30°．

(1)、求∠CBD的度数；

(2)、判断四边形OACB的形状，并说明理由．

查看试题解析

19. 电池技术是能源、信息和交通革命的关键．近年来，经国家推动，我国动力电池产业发展走在世界前列，根据图表信息，解答下列问题：

2016年中国动力电池正极材料出货量所占比例统计表

电池正极材料	所占百分比
三元电池正极材料
磷酸铁锂电池正极材料	73%
其他电池正极材料	5%

（数据来源：中商产业研究院中国动力电池正极材料行业现状深度研究与投资前景预测报告2022）

(1)、统计表中三元电池正极材料所占的百分比为；若依据此表制作扇形统计图，则三元电池正极材料所对应扇形的圆心角是度；

(2)、2017年到2022年三元电池正极材料出货量增长率的中位数为 %；

(3)、小致观察折线统计图后，认为2017年到2019年每年三元电池正极材料出货量都比磷酸铁锂电池正极材料出货量高，你同意他的说法吗？请结合统计表说明由．

查看试题解析

20. 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，以AB为直径的半圆的圆心为O，仅用无刻度的直尺在给定网格中完成画图：

(1)、请在图1中作出△ABC的AC边上的高BD；

(2)、请在图2中线段BC上确定一点F，使得OF∥AC；

(3)、请在图3中作出⊙O的切线AE．

查看试题解析
21. 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，图中的折线表示两车相距的距离（千米）与慢车行驶的时间x（小时）之间的函数关系．根据图象进行以下探究：

(1)、甲、乙两地之间相距的路程为千米；图中点B的实际意义为；

(2)、求线段BC所表示的y与x之间的函数解析式，并写出自变量x的取值范围；

(3)、当两车之间的距离不小于800千米时，直接写出x的取值范围．

查看试题解析
22. 在△ABC中，∠BAC＝90°，AB＝AC，点O在BC上（不与B、C重合），连接AO，F是线段AO上的点（不与A、O重合），∠EAF＝90°，AE＝AF，连接FE、FC、BE、BF．

(1)、如图①，若AO⊥BC，求证：BE＝BF；

(2)、如图②，将△AEF绕点A旋转，使边AF在∠BAC的内部，延长CF交AB与点G，交BE于点K．
①线段CF与BE的数量关系为；

②当△BEF为等腰直角三角形时， $\frac{A B}{B F}$ 的值为．

查看试题解析
23. 如图，AB是⊙O的直径，OA＝3．动点P从点A出发，在圆O上顺时针运动到终点B ，速度为每秒π个单位．同时动点Q从点B出发，在⊙O上沿顺时针方向运动，速度每秒3π个单位，当点P到达终点时，点Q也随之停止运动．连结OP、OQ．设点P的运动时间为t秒．

(1)、⊙O的周长为；

(2)、当点P与点Q重合时，求 $\overset{⌢}{A P}$ 所在的扇形的面积；

(3)、当OP⊥OQ时，求t的值；

(4)、作半径OP的垂直平分线交⊙O于点M、N，连结PQ．当PQ将线段MN分成1：2的两部分时，直接写出t的值．

查看试题解析
24. 在平面直角坐标系中，已知抛物线 $y = - \sqrt{3} x^{2} + 2 \sqrt{3} x + c$ 经过点 $A (- 2 ， - 5 \sqrt{3})$ ，点P在这条抛物线上，其横坐标为m．

(1)、求该抛物线所对应的函数关系式；

(2)、将抛物线上点A、P之间的部分（包括A、P两点）记为G．
①当m＝2时，求G上最高点与最低点的纵坐标之差；
②当G上最高点与最低点的纵坐标之差为9 $\sqrt{3}$ 时，求m的取值范围；

(3)、已知△BCD的顶点坐标分别为B（1，0）、C（3，0）、D（3，2 $\sqrt{3}$ ），当点P在x轴上方时，若点P到直线BC的距离与到直线BD的距离之和等于2 $\sqrt{3}$ ，请直接写出m的值．

查看试题解析