吉林省长春市南关区2023年中考数学四模试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的元件是( )A、
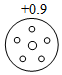 B、
B、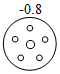 C、
C、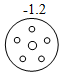 D、
D、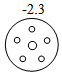 2. 2020年我国进行了第七次人口普查,数据显示,吉林省的常住人口数量约为24070000人,将24070000用科学记数法表示为( )A、24.07×106 B、24.07×107 C、2.407×107 D、0.2407×1083. 如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )
2. 2020年我国进行了第七次人口普查,数据显示,吉林省的常住人口数量约为24070000人,将24070000用科学记数法表示为( )A、24.07×106 B、24.07×107 C、2.407×107 D、0.2407×1083. 如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )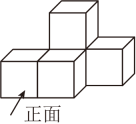 A、
A、 B、
B、 C、
C、 D、
D、 4. 若关于x的一元二次方程ax2-2x+3=0有两个不相等的实数根,则a的值可能是( )A、-1 B、 C、1 D、25. 如图,一辆自行车竖直摆放在水平地面上,如图是它的部分示意图,测得AB=60cm,∠B=50°,则点A到BC的距离为( )
4. 若关于x的一元二次方程ax2-2x+3=0有两个不相等的实数根,则a的值可能是( )A、-1 B、 C、1 D、25. 如图,一辆自行车竖直摆放在水平地面上,如图是它的部分示意图,测得AB=60cm,∠B=50°,则点A到BC的距离为( )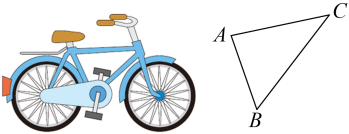 A、60sin50°cm B、60cos50°cm C、 D、60tan50°cm6. 如图,AB为⊙O的直径,点C在⊙O上,且 , 点D在上(不与点B、点C重合),则∠BDC的大小为( )
A、60sin50°cm B、60cos50°cm C、 D、60tan50°cm6. 如图,AB为⊙O的直径,点C在⊙O上,且 , 点D在上(不与点B、点C重合),则∠BDC的大小为( )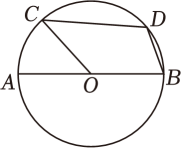 A、110° B、112.5° C、115° D、120°7. 如图,已知∠AOB=40°,按以下步骤作图:
A、110° B、112.5° C、115° D、120°7. 如图,已知∠AOB=40°,按以下步骤作图:
①在射线OA、OB上,分别截取OC、OD,使OC=OD;分别以点C点D为圆心,大于CD长为半径作圆弧,在∠AOB内两弧交于点E;作射线OE,连结DE.②分别以点D和点E为圆心、大于DE长为半径作圆弧,两弧交于点F和点G;作直线FG,分别交射线OA、OB于点H、点I.若∠OED=10°,则∠OHI的度数为( )
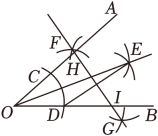 A、90° B、5° C、85° D、80°8. 如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球,小球在各自击出后2秒到达相同的最大飞行高度,若整个过程中,保持空中始终有1或2个小球(不考虑小球落地后再弹起),则t的取值范围是( )
A、90° B、5° C、85° D、80°8. 如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球,小球在各自击出后2秒到达相同的最大飞行高度,若整个过程中,保持空中始终有1或2个小球(不考虑小球落地后再弹起),则t的取值范围是( )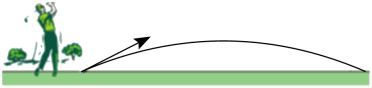 A、0<t<2 B、2≤t<4 C、1≤t<3 D、3≤t<5
A、0<t<2 B、2≤t<4 C、1≤t<3 D、3≤t<5二、填空题(本大题共6小题,每小题3分,共18分)
-
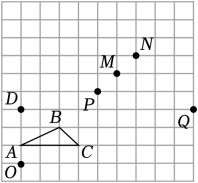
9. 分解因式:2x2﹣8y2=10. 不等式组的最大整数解为 .11. 一个正多边形的一个内角是与其相邻的一个外角的3倍,则这个正多边形的边数是 .12. 如图,在正方形网格图中,以O为位似中心,作△ABC的位似图形,若点D是点A的对应顶点,则点B的对应顶点是点 .
 13. 如图,在△ABC中,∠C=60°,将△ABC绕点A顺时针旋转得到△ADE,点C的对应点E恰好落在边BC上.若AC=5,则CE= .
13. 如图,在△ABC中,∠C=60°,将△ABC绕点A顺时针旋转得到△ADE,点C的对应点E恰好落在边BC上.若AC=5,则CE= .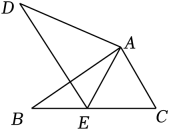 14. 如图,在平面直角坐标系中,点P在反比例函数y= (x>0)的图象上,点A,B在x轴上,且PA⊥PB,垂足为P,PA交y轴于点C,AO=BO=BP,△ABP的面积是2,则k的值是 .
14. 如图,在平面直角坐标系中,点P在反比例函数y= (x>0)的图象上,点A,B在x轴上,且PA⊥PB,垂足为P,PA交y轴于点C,AO=BO=BP,△ABP的面积是2,则k的值是 .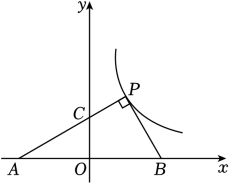
三、解答题(本大题共10小题,共78分)
-
15. 先化简,再求值: , 从 -2,-1,1,2中选取一个合适的数作为x的值代入求值.16. 《九章算术》是我国古代科技著作乃至世界古代数学著作中一颗璀璨的明珠,其中“损益术”记载:今有上禾五秉,损实一斗一升,当下禾七秉:上禾七秉,损实二斗五升,当下禾五秉.问:上、下禾实一秉各几何?译文为:5捆上等禾所得谷粒减去1斗1升(1斗=10升)后,相当于7捆下等禾所得谷粒;7捆上等禾所得谷粒减去2斗5升后,相当于5捆下等禾所得谷粒.则1捆上等禾和1捆下等禾各得谷粒多少升?请解决此问题.17. 如图,在▱ABCD中,点E是AD的中点,连接CE并延长,交BA的延长线于点F.求证:FA=AB.
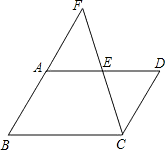 18. 某班同学分组做概率试验,试验要求:在一个不透明的口袋中装有n个红球和1个白球,每个小球除颜色不同外其余均相同,从口袋中摸出一个小球,记下颜色后将其放回袋中并搅匀,不断重复摸球并记录.
18. 某班同学分组做概率试验,试验要求:在一个不透明的口袋中装有n个红球和1个白球,每个小球除颜色不同外其余均相同,从口袋中摸出一个小球,记下颜色后将其放回袋中并搅匀,不断重复摸球并记录.
下表是统计汇总各小组数据后获得的全班数据统计表:摸球的次数
500
1000
1500
2000
2500
3000
摸到白球的频数
139
318
525
658
829
998
摸到白球的频率
0.278
0.318
0.35
0.329
0.332
0.333
(1)、根据试验所得的摸到白球的频率,得到n的值为 .(2)、在试验要求的条件下,用画树状图(或列表)的方法19. 图①、图②、图③均是7×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,按下列要求作图:(不写作法,保留画图痕迹)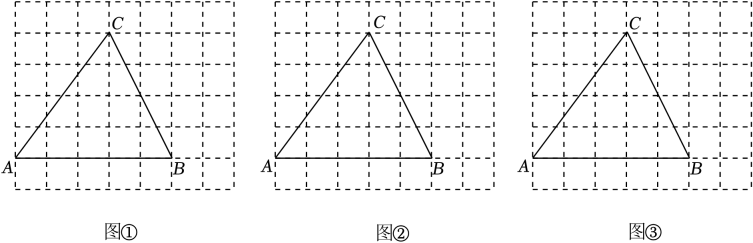 (1)、在图①中,在BC边上找一点D,连结AD,使AD平分∠A.(2)、在图②中,在AC边上找一点E,连结BE,使BE⊥AC于点E.(3)、在图③中,在AB边上找一点F,连结CF,使∠ACF=45°.20. 2022年是党和国家历史上极为重票的一年,面对风高浪急的国际环境和艰巨繁重的国内改革发展稳定任务,全国人民同心块力,顺利完成了经济保持增长,发展质量稳步提升的目标.2023年2月28日,国家统计局发布了《2022年国民经济和社会发展统计公报》,以下材料是公报中的部分内容.
(1)、在图①中,在BC边上找一点D,连结AD,使AD平分∠A.(2)、在图②中,在AC边上找一点E,连结BE,使BE⊥AC于点E.(3)、在图③中,在AB边上找一点F,连结CF,使∠ACF=45°.20. 2022年是党和国家历史上极为重票的一年,面对风高浪急的国际环境和艰巨繁重的国内改革发展稳定任务,全国人民同心块力,顺利完成了经济保持增长,发展质量稳步提升的目标.2023年2月28日,国家统计局发布了《2022年国民经济和社会发展统计公报》,以下材料是公报中的部分内容.材料一:如图是2018年到-2022年全年国内生产总值及其增长速度统计图.
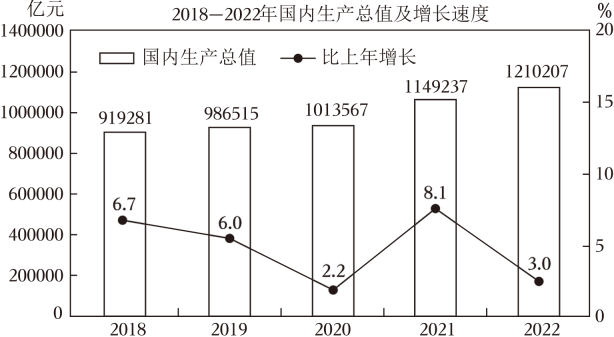
2022年是党和国家历史上极为重票的一年,面对风高浪急的国际环境和艰巨繁重的国内改革发展稳定任务,全国人民同心块力,顺利完成了经济保持增长,发展质量稳步提升的目标.2023年2月28日,国家统计局发布了《2022年国民经济和社会发展统计公报》,以下材料是公报中的部分内容.
根据以上信息回答下列问题:
(1)、从2018年到2022年,全年国内生产总值增长最快的是 年,从2018年到2022年,全年国内生产总值增长率的中位数是 %.(2)、在十四届全国人大一次会议上,李克强总理在政府工作报告中指出,2023年全年国内生产总值增长目标为5% ,请以此估计2023年全年国内生产总值. (结果精确到万亿元)(3)、小明同学阅读了材料二,发现如果将2022年的第一、二、三产业的增长率求平均数 , 这与2022年全年国内生产总值增长速度3.0%不符,请说明原因.21. 校运会上,每班选派一位男同学和一位女同学参加100米运球比赛,男同学甲与女同学乙同时从起点出发,运球沿同一路线匀速向终点前进,甲先到达终点放下球后立即原路返回接力乙同学,并与乙同学一起到达终点.甲、乙两位同学距出发地的路程y(米)与甲的运动时间x(秒)之间的函数关系如图所示.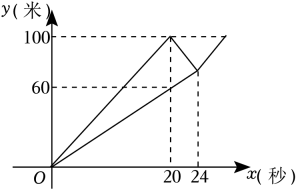 (1)、求甲同学从终点返回到与乙同学相遇过程中,甲同学距出发地的路程y与x之间的函数关系式.(2)、若甲同学与乙同学相遇后,改由甲同学运球,两人仍以甲第一次到达终点前的速度一起前往终点,则两人到达终点的时间为 秒.22. 综合与实践
(1)、求甲同学从终点返回到与乙同学相遇过程中,甲同学距出发地的路程y与x之间的函数关系式.(2)、若甲同学与乙同学相遇后,改由甲同学运球,两人仍以甲第一次到达终点前的速度一起前往终点,则两人到达终点的时间为 秒.22. 综合与实践
【问题情境】
在数学活动课上,同学们以“折叠矩形”为主题开展数学活动.已知,在矩形ABCD中,AB=6,AD=10,点P是AB边上一点,将△APD沿直线PD折叠,点A的对应点为点E.
【操作发现】
(1)、如图①,当点P与点B重合时,过点E作EF∥AB,交BD于点F,连结AF,试判定四边形ABEF的形状,并说明理由.(2)、操作二:如图②,当点E落在BC边上时,AP= .(3)、操作三:如图③,当点P为AB中点时,延长DE交BC于点G, 连结PG, 则tan∠PGB= .23. 如图,在扇形AOB中,圆心角∠AOB=90°,半径OA=2.点P为上一点,连结OP,过点A作AQ⊥OP于点Q.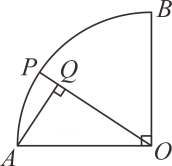 (1)、求的长.(2)、当点A、Q、B在同一条直线上时,求扇形AOP的面积.(3)、连结BQ,则线段BQ长的最小值为 .(4)、延长AQ,交直线OB于点C,若点Q为线段AC的三等分点,直接写出AC的长。24. 如图①,在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3), 抛物线的对称轴为直线x=1, 过B、C两点作直线l,点P在抛物线上, 且在直线l下方, 连结AP,交BC于点Q.
(1)、求的长.(2)、当点A、Q、B在同一条直线上时,求扇形AOP的面积.(3)、连结BQ,则线段BQ长的最小值为 .(4)、延长AQ,交直线OB于点C,若点Q为线段AC的三等分点,直接写出AC的长。24. 如图①,在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3), 抛物线的对称轴为直线x=1, 过B、C两点作直线l,点P在抛物线上, 且在直线l下方, 连结AP,交BC于点Q.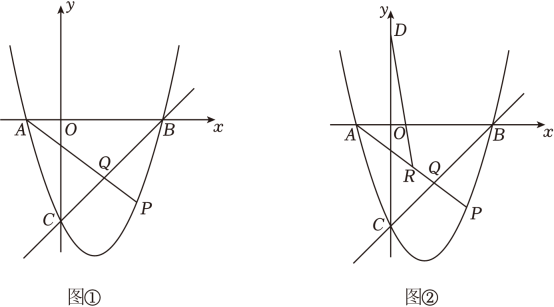 (1)、求b和c的值;(2)、求点A和点B的坐标,并直接写出直线l的表达式;(3)、求的最大值,及此时点P的坐标;(4)、如图②,点C关于x轴的对称点为点D,点R在线段AQ上 , 且AR=3QR, 连接DR,则DR+ AQ的最小值为 .
(1)、求b和c的值;(2)、求点A和点B的坐标,并直接写出直线l的表达式;(3)、求的最大值,及此时点P的坐标;(4)、如图②,点C关于x轴的对称点为点D,点R在线段AQ上 , 且AR=3QR, 连接DR,则DR+ AQ的最小值为 .