吉林省松原市长岭一中、二中、五中2023年中考模拟数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列各式计算结果是负数的是( )A、 B、 C、 D、2. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )A、0.28×1013 B、2.8×1011 C、2.8×1012 D、28×10113. 如图所示的几何体,其左视图是( )
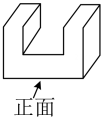 A、
A、 B、
B、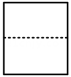 C、
C、 D、
D、 4. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 如图,在下列条件中,能够证明的条件是( )
4. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 如图,在下列条件中,能够证明的条件是( ) A、 B、 C、 D、6. 如图,四边形是的内接四边形, , 则的度数是( )
A、 B、 C、 D、6. 如图,四边形是的内接四边形, , 则的度数是( )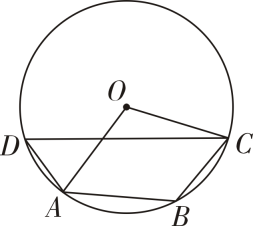 A、
A、
B、
C、
D、二、填空题(本大题共8小题,共24.0分)
-
7. 计算: .8. 计算 .9. 计算结果是 .10. 端午节是中国传统节日,人们有吃粽子的习俗利群商厦从月日起开始打折促销,肉粽六折,白粽七折,打折前购买盒肉粽和盒白粽需元,打折后购买盒肉粽和盒白粽需元设打折前每盒肉粽的价格为元,每盒白粽的价格为元,则可列方程组 .11. 如图,正方形与正方形起始时互相重合,现将正方形绕点逆时针旋转.设旋转角 , 则当时,正方形的顶点落在直线上.
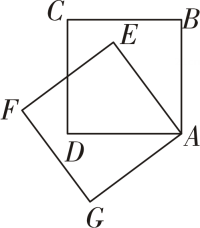 12. 如图,在中, , , 尺规作图作出的垂直平分线与交于点 , 则的度数为 .
12. 如图,在中, , , 尺规作图作出的垂直平分线与交于点 , 则的度数为 . 13. 为了估算河的宽度,我们可以在河对岸选定一个目标点 , 在近岸取点和 , 使点 , , 共线且直线与河岸垂直,然后在过点且与垂直的直线上选择适当的点 , 确定与过点且垂直的直线的交点已测得 , , , 则河宽
13. 为了估算河的宽度,我们可以在河对岸选定一个目标点 , 在近岸取点和 , 使点 , , 共线且直线与河岸垂直,然后在过点且与垂直的直线上选择适当的点 , 确定与过点且垂直的直线的交点已测得 , , , 则河宽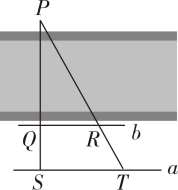 14. 如图,在扇形中, , 平分交于点 , 点为半径的中点.若 , 则阴影部分的面积为 .
14. 如图,在扇形中, , 平分交于点 , 点为半径的中点.若 , 则阴影部分的面积为 .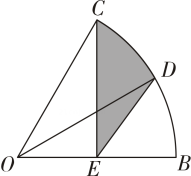
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
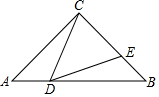
15. 先化简,再求值: , 其中 .16. 如图,在中, , D、E分别为、上一点,.若 , 求证:.
 17. 某校开展以“奋斗百年路启航新征程”为主题的活动来庆祝建党百年.活动分为两个阶段:第一阶段是宣讲红色故事,有以党建党史、文化传承、人物传记为素材的个宣讲项目分别用、、表示;第二阶段是主题文艺创作,有文学创作、美术创作、舞蹈创作、音乐创作个项目分别用、、、表示要求参加人员在每个阶段各随机抽取一个项目完成.若小明参加该活动,请用画树状图或列表的方法列出小明参加项目的所有可能的结果,并求小明恰好抽中项目和的概率.18. 在生产操作中,有些化工原料对人体有害,所以需要用机器人来搬运.现有 , 两种机器人,型机器人比型机器人每小时多搬运 , 型机器人搬运所用时间与型机器人搬运所用时间相等,则两种机器人每小时分别搬运多少化工原料?19. 如图,在的方格纸中,线段的端点均在格点上,请按要求画图.
17. 某校开展以“奋斗百年路启航新征程”为主题的活动来庆祝建党百年.活动分为两个阶段:第一阶段是宣讲红色故事,有以党建党史、文化传承、人物传记为素材的个宣讲项目分别用、、表示;第二阶段是主题文艺创作,有文学创作、美术创作、舞蹈创作、音乐创作个项目分别用、、、表示要求参加人员在每个阶段各随机抽取一个项目完成.若小明参加该活动,请用画树状图或列表的方法列出小明参加项目的所有可能的结果,并求小明恰好抽中项目和的概率.18. 在生产操作中,有些化工原料对人体有害,所以需要用机器人来搬运.现有 , 两种机器人,型机器人比型机器人每小时多搬运 , 型机器人搬运所用时间与型机器人搬运所用时间相等,则两种机器人每小时分别搬运多少化工原料?19. 如图,在的方格纸中,线段的端点均在格点上,请按要求画图. (1)、如图 , 画出一条线段 , 使 , 在格点上;
(1)、如图 , 画出一条线段 , 使 , 在格点上;
(2)、如图 , 画出一条线段 , 使 , 互相平分, , 均在格点上;
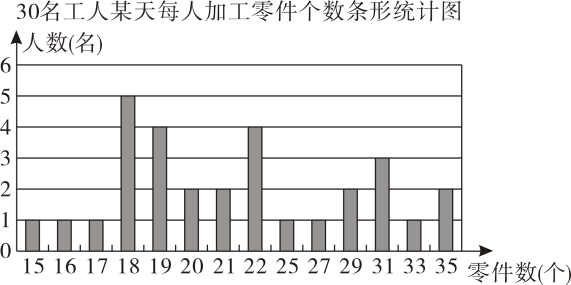
(3)、如图 , 以 , 为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.20. 某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查该部门随机抽取了名工人某天每人加工零件的个数,数据如下:整理上面数据,得到如图条形统计图;
样本数据的平均数、众数、中位数如表所示:统计量
平均数
众数
中位数
数值
根据以上信息解答下列问题:
(1)、上表中众数的值为 ;
(2)、为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适;填“平均数”、“众数“或“中位数”
(3)、该部门规定:每天加工零件的个数达到或超过个的工人为生产能手若该部门有名工人,试估计该部门生产能手的人数.21. 某老年活动中心欲在一房前高的前墙上安装一遮阳篷 , 使正午时刻房前能有宽的阴影处以供纳凉.假设此地某日正午时刻太阳光与水平地面的夹角为 , 遮阳篷与水平面的夹角为如图为侧面示意图,请你求出此遮阳篷的长度结果精确到参考数据: , , ; , ,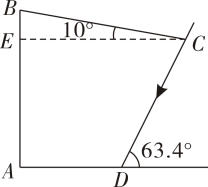 22. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与y轴交于点B,与x轴交于点 .
22. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与y轴交于点B,与x轴交于点 .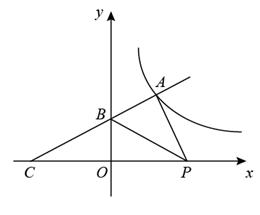 (1)、求k与m的值;(2)、 为x轴上的一动点,当△APB的面积为 时,求a的值.23. 在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车与C地的距离 (单位:km),(单位:km)与甲车行驶时间t(单位:h)之间的函数关系如图.请根据所给图象解答下列问题:
(1)、求k与m的值;(2)、 为x轴上的一动点,当△APB的面积为 时,求a的值.23. 在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车与C地的距离 (单位:km),(单位:km)与甲车行驶时间t(单位:h)之间的函数关系如图.请根据所给图象解答下列问题: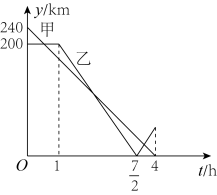 (1)、甲车的行驶速度为km/h,乙车的行驶速度为km/h;(2)、当时,求乙车与C地的距离与甲车行驶时间t之间的函数关系式;(3)、当乙车出发小时,两车相遇;24. 【问题情境】
(1)、甲车的行驶速度为km/h,乙车的行驶速度为km/h;(2)、当时,求乙车与C地的距离与甲车行驶时间t之间的函数关系式;(3)、当乙车出发小时,两车相遇;24. 【问题情境】
如图 , 点为正方形内一点, , 将绕点按顺时针方向旋转 , 得到点的对应点为点延长交于点 , 连接 .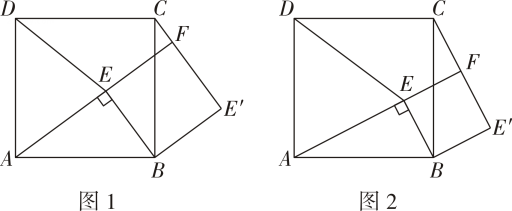 (1)、四边形的形状是 ;(2)、若 , , 则正方形的面积为 ;
(1)、四边形的形状是 ;(2)、若 , , 则正方形的面积为 ;
(3)、如图 , 若 , 请猜想线段与的数量关系并加以证明.25. 如图,在中, , , , 动点从点出发,以的速度沿方向向终点运动,当点不与点重合时,过点作于点 , , 过点作 , 与相交于点设点的运动时间为 . (1)、线段的长;用含的代数式表示
(1)、线段的长;用含的代数式表示
(2)、当点落在边上时,求的值;
(3)、设与重叠部分的面积为求关于的函数解析式,并直接写出自变量的取值范围.26. 如图 , 已知抛物线与轴交于点和点 , 与轴交于点 , .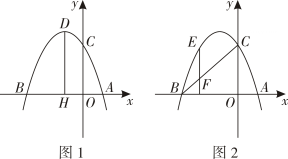 (1)、求抛物线的解析式.
(1)、求抛物线的解析式.
(2)、如图 , 点为第二象限抛物线上一动点,轴与交于 , 求的最大值,并说明此时的面积是否最大.
(3)、已知点 , , 连接若抛物线向上平移个单位长度时,与线段只有一个公共点,请求出的取值范围.