吉林省白城市大安市2023年中考模拟数学考试试卷(5月份)
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 3的相反数是( )A、 B、3 C、 D、2. 吉林省全力打造国家级能源生产基地,“十四五”期间共个项目纳入国家抽水蓄能选点规划,装机规模千瓦数据用科学记数法表示为( )A、 B、 C、 D、3. 不等式的解集是( )A、 B、 C、 D、4. 如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
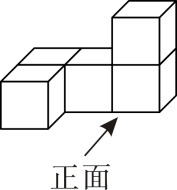 A、
A、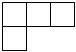 B、
B、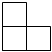 C、
C、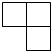 D、
D、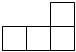 5. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )
5. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )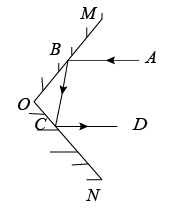 A、 B、 C、 D、6. 如图,是的直径,、是上的两点,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,是的直径,、是上的两点,若 , 则的度数为( )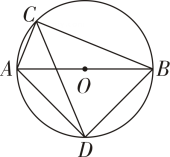 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
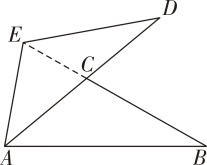
7. 计算: .8. 分解因式: .9. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为.10. 关于的一元二次方程有两个相等的实数根,则 .11. 篮球每个元,排球每个元,如果学校要购买个篮球、个排球,一共需要支付 元用含有、的代数式表示 .12. 如图,绕点逆时针旋转得到 , 点在上,点的对应点在的延长线上,若 , 则 .
 13. 如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为 m.
13. 如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为 m.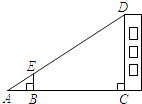 14. 如图,以边长为2的等边顶点A为圆心、一定的长为半径画弧,恰好与边相切,分别交于D,E,则图中阴影部分的面积是 .
14. 如图,以边长为2的等边顶点A为圆心、一定的长为半径画弧,恰好与边相切,分别交于D,E,则图中阴影部分的面积是 .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 先化简,再求值: , 其中 .16. 如图,已知平分 , 求证:≌ .
 17. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回搅匀,再从中随机摸出一个小球记下标号.规定当两次摸出的小球标号相同时中奖,求中奖的概率,请用画树状图或列表法的方法求中奖的概率.18. 图 , 图均是的正方形网格,点、、均在格点上,请在给定的网格中用无刻度的直尺作图,并保留作图痕迹.
17. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回搅匀,再从中随机摸出一个小球记下标号.规定当两次摸出的小球标号相同时中奖,求中奖的概率,请用画树状图或列表法的方法求中奖的概率.18. 图 , 图均是的正方形网格,点、、均在格点上,请在给定的网格中用无刻度的直尺作图,并保留作图痕迹.
 (1)、在图中,作的中线;
(1)、在图中,作的中线;
(2)、在图中,作的高线 .19. 每年的月日是全国爱眼日,眼睛是人类感官中最重要的器官之一,不当的用眼习惯会影响健康某校在爱眼日到来之际,计划购买、两类护眼用具,已知类护眼用具每个的价格比类护眼用具便宜元,且用元购买的类护眼用具的个数与用元购买的类用具的个数相同求、两类护眼用具的单价各是多少元?20. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于点、 , 与反比例函数的图象交于点 , 连接已知点 , 的面积是 .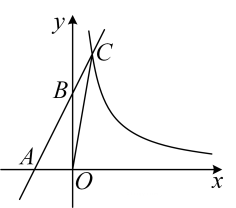 (1)、求、的值;
(1)、求、的值;
(2)、求的面积.21. 如图,艘轮船位于灯塔的北偏东方向,距离灯塔海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处这时,处距离灯塔有多远?
结果保留整数,参考数据: , , , 22. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟按照完成时间分成五组:组“”,组“”,组“”,组“”,组“”将收集的数据整理后,绘制成如下两幅不完整的统计图.
22. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟按照完成时间分成五组:组“”,组“”,组“”,组“”,组“”将收集的数据整理后,绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)、这次调查的样本容量是 , 请补全条形统计图;
(2)、在扇形统计图中,组的圆心角是度,本次调查数据的中位数落在组内;
(3)、若该校有名学生,请你估计该校每天完成书面作业不超过分钟的学生人数.23. 已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.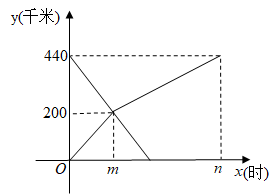 (1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.24. 某数学活动小组在学完特殊的平行四边形之后,针对矩形中的折叠问题进行了研究.
(1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.24. 某数学活动小组在学完特殊的平行四边形之后,针对矩形中的折叠问题进行了研究.
如图 , 在矩形中, , , 点为边上一点,将矩形沿折叠,点为点折叠后的对应点,过点作 , 交折痕于点 , 连接 .
 (1)、猜想四边形的形状,并证明你的结论;
(1)、猜想四边形的形状,并证明你的结论;
(2)、如图 , 连接 , 当点落在上时,的长为 用含的代数式表示;
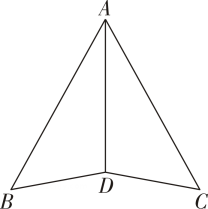
(3)、如图 , 当点落在上时,若 , 请直接写出的长.25. 如图,在等腰中, , , 动点由点出发,沿边以的速度运动到点停止,过作交或边于点 , 过点作的平行线与过点作的平行线交于点 .
 (1)、填空:;
(1)、填空:;
(2)、当点在边上时,求的值;
(3)、与重合部分图形的面积为 , 用含的代数式表示 , 并直接写出的取值范围.26. 如图,在平面直角坐标系中,为坐标原点,二次函数的图象经过点点是抛物线上一点不与点重合 , 其横坐标为以为对角线作矩形 , 垂直于轴.
 (1)、求抛物线的解析式和顶点坐标;
(1)、求抛物线的解析式和顶点坐标;
(2)、当矩形内部的图象从左到右逐渐上升时,求的取值范围;
(3)、当矩形内部的图象包括边界的最高点纵坐标与最低点的纵坐标之差为时,求的值;
(4)、设点的纵坐标为 , 当该抛物线上有四个点到直线的距离是到直线距离的倍时,直接写出的取值范围.