吉林省白城市通榆县2023年中考三模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的倒数是( )A、 B、 C、 D、2. 某物体如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. “与的积加上不小于”用不等式表示是( )A、 B、 C、 D、4. 同学们做广播操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面同学的后后脑勺,这其中用到的数学原理是( )A、垂线段最短 B、经过一点有无数条直线
3. “与的积加上不小于”用不等式表示是( )A、 B、 C、 D、4. 同学们做广播操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面同学的后后脑勺,这其中用到的数学原理是( )A、垂线段最短 B、经过一点有无数条直线
C、两点之间,线段最短 D、经过两点,有且只有一条直线5. 如图,将一张长方形纸条沿某条直线折叠,若 , 则( ) A、
A、
B、
C、
D、6. 如图,在中, , 是劣弧的中点,是优弧任意一点,连接 , , 则的度数是( ) A、或
A、或
B、
C、
D、二、填空题(本大题共8小题,共24.0分)
-
7. 分解因式: .8. 每到春天,人们在欣赏柳绿桃红的同时,也被飞舞的柳絮所烦恼,据了解柳絮纤维的直径约为 , 把写成科学记数法的形式为 .9. 计算: .10. 如果关于的一元二次方程有两个不相等的实数根,那么的值可以是 . (写出一个值即可)11. 如图,该图形绕其中心旋转能与其自身完全重合,则其旋转角最小为 度
 12. 为了营造自觉爱绿、植绿、护绿的浓厚氛围,甲、乙两组学生踊跃参加植树造林活动已知甲组每小时比乙组多植棵树,甲组植棵树用时与乙组植棵树用时相同设甲组每小时植棵树,根据题意列出分式方程: .13. 如图是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了在图中,杠杆的端被向上翘起的距离 , 动力臂与阻力臂满足与相交于点 , 要把这块石头翘起,至少要将杠杆的点向下压 .
12. 为了营造自觉爱绿、植绿、护绿的浓厚氛围,甲、乙两组学生踊跃参加植树造林活动已知甲组每小时比乙组多植棵树,甲组植棵树用时与乙组植棵树用时相同设甲组每小时植棵树,根据题意列出分式方程: .13. 如图是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了在图中,杠杆的端被向上翘起的距离 , 动力臂与阻力臂满足与相交于点 , 要把这块石头翘起,至少要将杠杆的点向下压 .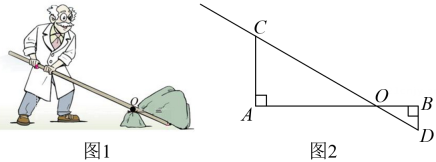 14. 如图,在中,为直径,点是上的一点,连接、 , 以为圆心,的长为半径作弧,恰好经过点 , 若 , 则图中阴影部分的周长是 结果保留根号和 .
14. 如图,在中,为直径,点是上的一点,连接、 , 以为圆心,的长为半径作弧,恰好经过点 , 若 , 则图中阴影部分的周长是 结果保留根号和 .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 先化简,再求值: , 其中 .16. 如图,在中,为延长线上的一点, , 求证:是等边三角形.
 17. 周末同学们和部分家长代表共人组团到动物园进行春游活动已知动物园的门票销售标准是:家长成人票元张,学生门票是成人票价的五折该团队购门票共花费元问该团队家长代表和学生分别有多少人?18. 一个不透明的口袋中装有个小球,这四个小球上分别标有数字、、、 , 这四个小球除了标的数字不同其余完全相同若小刚一次摸出两个球,用画树状图或列表的方法求两个球上的数字之积为负数的概率.19. 图、图均是的正方形网格,每个小正方形的边长均为 , 小正方形的顶点称为格点用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上.
17. 周末同学们和部分家长代表共人组团到动物园进行春游活动已知动物园的门票销售标准是:家长成人票元张,学生门票是成人票价的五折该团队购门票共花费元问该团队家长代表和学生分别有多少人?18. 一个不透明的口袋中装有个小球,这四个小球上分别标有数字、、、 , 这四个小球除了标的数字不同其余完全相同若小刚一次摸出两个球,用画树状图或列表的方法求两个球上的数字之积为负数的概率.19. 图、图均是的正方形网格,每个小正方形的边长均为 , 小正方形的顶点称为格点用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上.
 (1)、在图中,以线段为一边画一个菱形;
(1)、在图中,以线段为一边画一个菱形;
(2)、在图中,以点为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.20. 某校科技小组在一次野外考察中遇到一片烂泥湿地为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木板,构筑成一条临时近道每块木板对地面的压强是木板面积的反比例函数,其图象如图所示.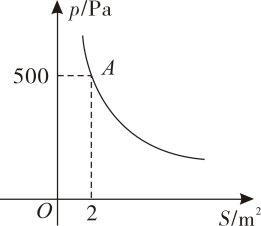 (1)、请根据图象直接写出反比例函数的解析式;
(1)、请根据图象直接写出反比例函数的解析式;
(2)、如果要求压强不超过 , 求选用的木板的面积至少要多大?21. 如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成角的楼梯 , 和一段水平平台构成,米,米,米求:天桥高度及引桥水平跨度 .
参考数据:取 , , 22. 某学校举办了以“生态文明与环境保护”为主题的相关知识测试,为了了解学生对“生态文明与环境保护”相关知识的掌握情况,随机抽取名学生的测试成绩百分制,成内绩取整数并进行整理,数据分成组,分别为 , , , , , 信息如下:
22. 某学校举办了以“生态文明与环境保护”为主题的相关知识测试,为了了解学生对“生态文明与环境保护”相关知识的掌握情况,随机抽取名学生的测试成绩百分制,成内绩取整数并进行整理,数据分成组,分别为 , , , , , 信息如下:
信息:名学生的测试成绩的频数分布直方图如图所示.
信息:在这一组的成绩如下:单位:分根据以上信息,解答下列问题.(1)、在这次测试中,成绩的中位数是 分,成绩低于分的人数占测试人数要的百分比为 ;
(2)、这次测试成绩的平均数是分,小颖的测试成绩是分小亮说:“小颖的成绩高于平均数,所以小颖的成绩高于一半学生的成绩”你认为小亮的说法正确吗?请说明理由.23. 某车间甲、乙两台机器共生产个零件,两台机器同时加工一段时间后,甲机器出现故障,维修一段时间后仍按原来的效率加工,已知甲机器每天加工个零件,如图是表示未生产零件的个数个与乙机器工作时间天之间的函数图象. (1)、乙机器每天加工 个零件,甲机器维修了 天;
(1)、乙机器每天加工 个零件,甲机器维修了 天;
(2)、求未生产零件的个数个与乙机器工作时间天之间的函数关系式;
(3)、当甲、乙两台机器共生产个零件时,乙机器加工了多少天?24. (1)、【探究问题】阅读并补全解题过程
(1)、【探究问题】阅读并补全解题过程
如图 , 在四边形中, , 点是边的中点, , 求证:平分 .
张某某同学受到老师说过的“有中点,延长加倍构造全等”的启发,延长交射线于点 , 请你依据该同
学的做法补全证明过程.
证明:延长交射线于点 .(2)、【应用】如图 , 在长方形中,将沿直线折叠,若点恰好落在边的中点处,直接写出的度数;
(3)、【拓展】如图 , 在正方形中,为边的中点,将沿直线折叠,点落在正方形内部的点处,延长交于点 , 延长交于点 , 若正方形的边长为 , 直接写出的值.25. 如图 , 在中, , , 动点从点出发,沿折线以每秒个单位长度的速度向终点运动,当点不与点和点重合时,过点作于点设点的运动时间为秒. (1)、用含的代数式表示线段的长.
(1)、用含的代数式表示线段的长.
(2)、当线段将分成的两部分图形中存在轴对称图形时,求的值.
(3)、设线段扫过图形的面积为 , 求与之间的函数关系式.
(4)、如图 , 以为斜边向上作等腰直角三角形连结 , 当线段的垂直平分线平行于的一边时,直接写出的值.26. 如图,抛物线经过点 , 点 , 与轴交于点 , 点在射线上运动,过点作直线轴,交抛物线于点 , 点在点的左侧 .
 (1)、求该抛物线的解析式和对称轴;
(1)、求该抛物线的解析式和对称轴;
(2)、若 , 求点的坐标;
(3)、若抛物线的顶点关于直线的对称点为点 , 当点到轴的距离等于时,求出所有符合条件的线段的长;
(4)、以点为旋转中心,将点绕点顺时针旋转得到点 , 直接写出点落在抛物线上时点的坐标.