安徽省宿州市泗县2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的绝对值是( )A、 B、 C、 D、2. 根据安徽历年高考报名人数预测,年参加高考报名的预计有万人,高考报名人数呈逐年上升趋势,其中万用科学记数法表示为( )A、 B、 C、 D、3. 计算:的结果是( )A、 B、 C、 D、4. 如图所示,该几何体的左视图是( )
 A、
A、
B、
C、
D、 5. 将一把含角的三角尺和一把长方形直尺按如图所示摆放,若 , 则的度数为( )
5. 将一把含角的三角尺和一把长方形直尺按如图所示摆放,若 , 则的度数为( ) A、
A、
B、
C、
D、6. 甲无人机从地面起飞,乙无人机从距离地面高的楼顶起飞,甲、乙两架无人机所在的位置距离地面的高度单位:与无人机上升的时间单位:之间的关系如图所示,当无人机上升时间为时,两架无人机的高度差为( ) A、
A、
B、
C、
D、7. 若 , , 为互不相等的实数,且 , 则下列结论正确的是( )A、 B、 C、 D、8. 将标有“最”“美”“安”“徽”的四个小球装在一个不透明的口袋中每个小球上仅标一个汉字 , 这些小球除所标汉字不同外,其余均相同从中随机摸出两个球,则摸到的球上的汉字可以组成“安徽”的概率是( )A、 B、 C、 D、9. 如图,在中, , , , 则的长为( )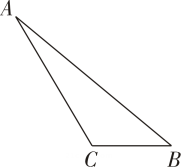 A、 B、 C、 D、10. 如图,在矩形和矩形中, , 且 , 连接交于点 , 连接交于点 , 交于点 , 则下列结论不正确的是( )
A、 B、 C、 D、10. 如图,在矩形和矩形中, , 且 , 连接交于点 , 连接交于点 , 交于点 , 则下列结论不正确的是( )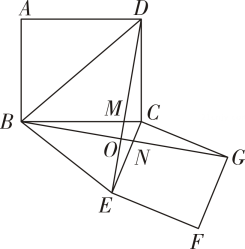 A、
A、
B、当时,
C、当时,∽
D、当时,二、填空题(本大题共4小题,共20.0分)
-
11. 计算: .12. 若是关于的一元二次方程的解,则 .13. 如图,点在反比例函数的图象上,连接交反比例函数的图象于点 , 若点的横坐标为 , 则点的横坐标为 .
 14. 如图,正方形的边长为 , 点 , 分别在 , 上将该正方形沿折叠,使点落在边上的点处,折痕与相交于点 .
14. 如图,正方形的边长为 , 点 , 分别在 , 上将该正方形沿折叠,使点落在边上的点处,折痕与相交于点 . (1)、若是的中点,则的长为 ;
(1)、若是的中点,则的长为 ;
(2)、若为的中点,随着折痕位置的变化,的最小值为 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 解不等式: .16. 在平面直角坐标系中,三个顶点的坐标分别是 , ,
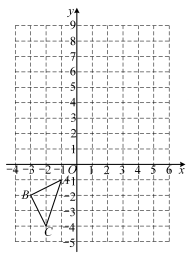
⑴将关于轴对称得到 , 画出;
⑵将中的绕点顺时针旋转得到 , 画出 , 并写出点的坐标.17. 观察下列等式:第个等式:;
第个等式:;
第个等式:;
按照以上规律,解决下列问题:(1)、写出第个等式: ;
(2)、写出你猜想的第个等式用含的等式表示 , 并证明.18. 九章算术是中国古代算经十书最重要的一部,它的出现标志中国古代数学形成了完整的体系,其中有一道阐述“盈不足数”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四其意思可以理解为现在有一些人共同买一个物品,如果每人出钱,还多出钱;如果每人出钱,则还差钱.(1)、若共同买这一物品的人数为人,则根据每人出钱,还多出钱,表示该物品的价格为 钱用含的式子表示;
(2)、计算购买个该物品所需的钱数.19. “儿童散学归来早,忙趁东风放纸鸢”随着春季的来临,放风筝已成为孩子们的最爱周末小冬和爸爸一起去公园放风筝,如图,当小冬站在处时,风筝在空中的位置为点 , 仰角为 , 小冬站在处继续放线,当再放米长的线时,风筝飞到点处,此时点、离地面的高度恰好相等,点的仰角为 , 若小冬的眼睛与地面的距离为米,请计算风筝离地面的高度结果保留整数,参考数据: , ,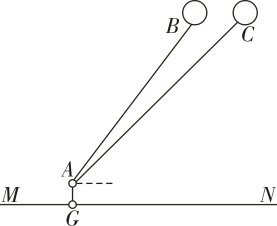 20. 如图,是的内接三角形,是圆外一点,连接 , , 连接交于点 .
20. 如图,是的内接三角形,是圆外一点,连接 , , 连接交于点 . (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、若 , 是的中点,求的长度.21. 今年月日是第八个“全民国家安全教育日”,为树立同学们的国家安全观、感悟新时代国家安全成就感,合肥某中学开展了以“国家安全我的责任”为主题的学习活动,并对此次学习结果进行了测试,调查小组随机抽取了份学生的测试成绩注:测试满分分,分数取整数 , 按测试成绩 , , , , 进行分组,将数据整理后得到如图不完整的频数分布直方图.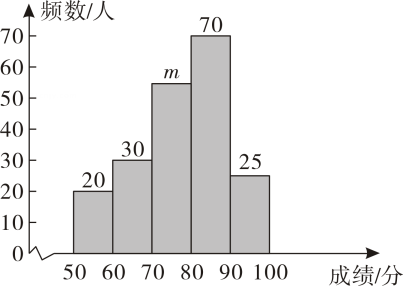 (1)、求频数分布直方图中的值;
(1)、求频数分布直方图中的值;
(2)、这名学生成绩的中位数会落在哪个分数段?直接写出结果
(3)、如果分以上为“优秀”,请估计全校名学生中,成绩为“优秀”的有多少人.