安徽省安庆市2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 实数的相反数是( )A、 B、 C、 D、2. 下列计算不正确的是( )A、 B、 C、 D、3. 魏晋南北朝时期,我国数学家祖冲之利用割圆术,求出圆周率约为 , 其与的误差小于其中用科学记数法可表示为( )A、 B、 C、 D、4. 如图,将一个正方体沿图示四条棱的中点切掉一部分,则该几何体的俯视图是( )
 A、
A、
B、
C、
D、 5. 下列分解因式正确的是( )A、 B、 C、 D、6. 已知关于的一元二次方程为常数 , 下列说法正确的是( )A、方程可能无实数根
5. 下列分解因式正确的是( )A、 B、 C、 D、6. 已知关于的一元二次方程为常数 , 下列说法正确的是( )A、方程可能无实数根
B、当时,方程的根为 ,
C、若 , 是方程的两个实数根,则
D、当时,方程的根为 ,7. 将一把直尺和一块含有的直角三角板按如图所示的位置摆放,若 , 则为( )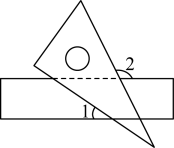 A、 B、 C、 D、8. 如图是某电路图,随机闭合开关 , , 中的任意个,能同时使两盏小灯泡发光的概率是( )
A、 B、 C、 D、8. 如图是某电路图,随机闭合开关 , , 中的任意个,能同时使两盏小灯泡发光的概率是( ) A、
A、
B、
C、
D、9. 已知实数 , , 满足 , , 则下列选项中正确的( )A、 , B、 , C、 , D、 ,10. 如图,正三角形的边长为 , 点从点开始沿着路线运动,过点作直线 , 垂足为点 , 连接 , 记点的运动路程为 , 的面积为 , 则关于的函数图象大致为( ) A、
A、
B、
C、
D、
二、填空题(本大题共4小题,共20.0分)
-
11. 不等式的解集为 .12. 如图,在中,平分 , 交于点 , 若 , , 则:为 .
 13. 如图,在中, , , , 点是斜边上一个动点,连接 , 过点作交直线于点 , 则当点从点运动到点时,点的运动路径长为 .
13. 如图,在中, , , , 点是斜边上一个动点,连接 , 过点作交直线于点 , 则当点从点运动到点时,点的运动路径长为 .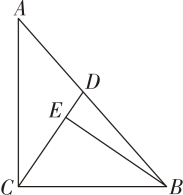 14. 已知抛物线:与直线:交于轴上同一点.(1)、的值为 .
14. 已知抛物线:与直线:交于轴上同一点.(1)、的值为 .
(2)、点是直线上的一个动点,将点向左移动个单位得到点 , 若线段与抛物线只有一个公共点,则点的横坐标的取值范围为 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算: .16. 如图,在的方格纸中,每个小正方形的边长为 , , , , , 均为格点, , 交于点 , 过 , , 三点的圆如图所示,请利用无刻度直尺找出该圆的圆心 , 并简要说明点的位置是如何找到的不要求证明 .
 17. 年安庆市为成功创建国家卫生城市,青年志愿者决定义务清除重达吨的垃圾开工后,附近居民主动参与到该项义务劳动中来,使清除垃圾的速度提高了倍,提前小时完成了任务,求青年志愿者原计划每小时清除多少吨垃圾?18. 设一个两位数可表示为 , 当取不同的值时,的平方如下:
17. 年安庆市为成功创建国家卫生城市,青年志愿者决定义务清除重达吨的垃圾开工后,附近居民主动参与到该项义务劳动中来,使清除垃圾的速度提高了倍,提前小时完成了任务,求青年志愿者原计划每小时清除多少吨垃圾?18. 设一个两位数可表示为 , 当取不同的值时,的平方如下:
第个等式:;
第个等式:;
第个等式:;
(1)、请写出第个等式: ;
(2)、根据上述规律,请写出的平方的一般性规律,并予以证明.19. 如图,某班数学兴趣小组用无人机在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为 , 测得点处的俯角为又经过人工测量得知操控者和教学楼的水平距离为米,则教学楼高度为多少米?结果精确到米, 20. 已知反比例函数与一次函数交于 , 两点,点的纵坐标为 .
20. 已知反比例函数与一次函数交于 , 两点,点的纵坐标为 . (1)、求一次函数解析式及与轴交点的坐标;
(1)、求一次函数解析式及与轴交点的坐标;
(2)、若点与点关于原点对称,求的面积.21. 年月开始,劳动课将正式成为中小学的一门独立课程,安庆市某中学提前尝试建立劳动教育实践基地,将劳动教育纳入日常教育教学中某日,学校从七、八年级班级管理的花圃中,分别随机抽取了个花圃对管理情况进行了评分满分分,数据分组为组, , 组: , 组: , 组: , 表示评分的分数 , 现将评分情况绘制成了不完整的统计图: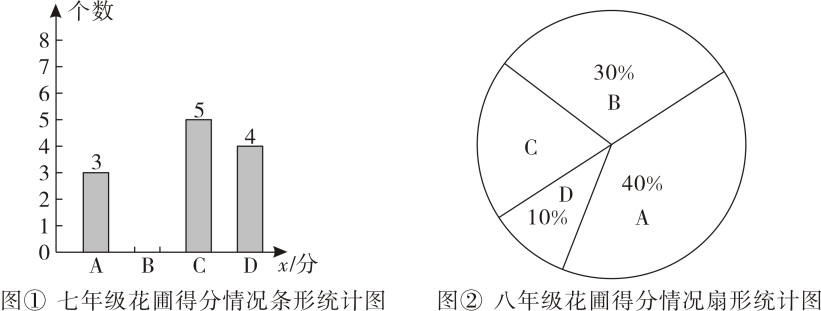 (1)、补全图中的条形统计图;图中组所对应的圆心角为 ▲ ;
(1)、补全图中的条形统计图;图中组所对应的圆心角为 ▲ ;
(2)、若八年级组得分情况为 , , , , , .
八年级组得分的方差为 ▲ ;
八年级个花圃得分的中位数为 ▲ 分;
(3)、若分以上为“五星花圃”,七、八年级各有个花圃,估计七、八年级的花圃中“五星花圃”共多少个?22. “龙池香尖”是怀宁县一款中国国家地理标志产品,素有:“扬子江心水,蒙山顶上茶”的美誉某茶庄以元的价格收购一批龙池香尖,为保护消费者的合法权益,物价部门规定每千克茶叶的利润不低于元,且不超过进价的 , 经过试销发现,日销量与销售单价元满足一次函数关系,部分数据统计如表:元
(1)、根据表格提供的数据,求出关于的函数关系式.
(2)、在销售过程中,每日还需支付其他费用元,当销售单价为多少时,该茶庄日利润最大,并求出最大利润.23. 正方形中,点是对角线上一点,连接 , 过点作的垂线分别交边 , 于 , , 交的延长线于点 , 作交于点 .
 (1)、求证:≌;
(1)、求证:≌;
(2)、连接 , .
求证:四边形是矩形;
如果点是的中点,和的面积分别是 , , 求的值.