安徽省滁州市2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 实数的绝对值是 , 的值是( )A、 B、 C、 D、2. 计算的结果是( )A、 B、 C、 D、3. 如图是一个三棱柱切去一部分后得到的几何体,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 古往今来,人类逐水而居,守住湿地造福子孙我国陆续将约万公顷的湿地纳入国家森林体系其中数据万用科学记数法表示为( )A、 B、 C、 D、5. 将一副三角板( , )按如图所示方式摆放,点F在 的延长线上,若 ,则 ( )
4. 古往今来,人类逐水而居,守住湿地造福子孙我国陆续将约万公顷的湿地纳入国家森林体系其中数据万用科学记数法表示为( )A、 B、 C、 D、5. 将一副三角板( , )按如图所示方式摆放,点F在 的延长线上,若 ,则 ( )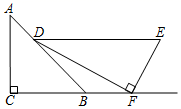 A、 B、 C、 D、6. 若关于的方程有实数根,则的取值范围是( )A、 B、 C、且 D、且7. 已知 ,则 的值等于( )A、1 B、0 C、 D、8. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( )
A、 B、 C、 D、6. 若关于的方程有实数根,则的取值范围是( )A、 B、 C、且 D、且7. 已知 ,则 的值等于( )A、1 B、0 C、 D、8. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( ) A、 B、 C、 D、9. 已知函数 , 当时,则函数的图象可能是下图中的( )A、
A、 B、 C、 D、9. 已知函数 , 当时,则函数的图象可能是下图中的( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在▱中, , , , 点为边上一动点,连接并延长至点 , 使得 , 以 , 为邻边构造▱ , 连接交于点当的长最小时,的长为( )
10. 如图,在▱中, , , , 点为边上一动点,连接并延长至点 , 使得 , 以 , 为邻边构造▱ , 连接交于点当的长最小时,的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共20.0分)
-
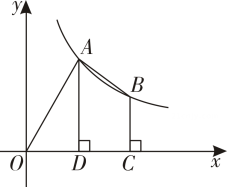
11. 已知 , , 则 .12. 某中学九年级班、班、班、班随机分成两批参加公益活动,每批两个班小明所在的九班被分在第一批的概率为 .13. 如图,在平面直角坐标系中,为坐标原点,点 , 在函数的图象上,过点作轴于点 , 过点作轴于点 , 连接 , 若 , 且四边形的面积为 , 则的值为 .
 14. 如图,在中, , , 点是上的一点,过点作交于点 , 将绕点逆时针方向旋转得到 , 连接 , .
14. 如图,在中, , , 点是上的一点,过点作交于点 , 将绕点逆时针方向旋转得到 , 连接 , . (1)、若 , 则 .
(1)、若 , 则 .
(2)、若 , 点是的中点,且点 , , 在一条直线上,则的长是 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算 .16. 在由边长为个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,是格点三角形顶点是网格线的交点 .
 (1)、画出关于点成中心对称的;
(1)、画出关于点成中心对称的;
(2)、画出将向左平移个单位长度得到的;
(3)、若点的坐标是 , 则点经过上述两种变换后的对应点的坐标是 .17. 中国古代数学著作张丘建算经中有“百钱买百鸡”问题,大意为:用文钱购买了只鸡,公鸡一只文钱,母鸡一只文钱,小鸡则一文钱只若公鸡买了只,求母鸡、小鸡各买了多少只请你解决上述问题.18. 观察下列等式:
第个等式: ,
第个等式: ,
第个等式: ,
第个等式: ,
按照以上规律,解决下列问题:(1)、写出第个等式: .
(2)、写出第个等式: ,并证明.19. 如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成角的楼梯、和一段水平平台构成.已知天桥高度米,引桥水平跨度米. (1)、求水平平台的长度;
(1)、求水平平台的长度;
(2)、若与地面垂直的平台立柱的高度为米,求两段楼梯与的长度之比.
参考数据:取 , ,20. 如图,是的直径,点 , 在上,且 , 连接 , 交于点 , 连接 , , . (1)、若 , 求的度数;
(1)、若 , 求的度数;
(2)、用尺规作图作出的角平分线交于点保留作图痕迹 , 并求证: .21. 某校为了解九年级学生的体质情况举行体育测试,以九年级班学生的体育测试成绩为样本,按 , , , 四个等级进行统计,并将统计结果绘制成如下的统计图:
说明:级:分分;级:分分;级:分分;级:分以下级成绩为优秀,级成绩为良好,级成绩为合格,级成绩为不合格
其中级成绩单位:分为:; , , , , , , , , , , , , , , , , , , ,
请你结合所给信息,解决下列问题:(1)、将条形统计图补充完整;
(2)、扇形统计图中级所在的扇形的圆心角度数是 ;九年级班学生的体育测试成绩的中位数是 ;(3)、若该校九年级有名学生,诪你用此样本估计体育测试中达到良好及良好以上的学生人数约为多少人.22. 【阅读理解】已知关于、的二次函数 , 它的顶点坐标为 , 故不论取何值时,对应的二次函数的顶点都在直线上,我们称顶点位于同一条直线上且形状相同的抛物线为同源二次函数,该条直线为根函数.(1)、【问题解决】若二次函数和是同源二次函数,求它们的根函数;(2)、已知关于、的二次函数: , 完成下列问题:
求满足二次函数的所有二次函数的根函数;
若二次函数与直线交于点 , 求点到轴的最小距离,请求出此时为何值?并求出点到轴的最小距离.23. 如图 , 在正方形中,点是对角线上一点不与点 , 重合 , 交边于点 , 连接 , 过点作交的延长线于点 , 连接 . (1)、求证:∽;(2)、求的度数;(3)、若正方形的边长为 , 点是延长线上一点,交的延长线于点 , 且恰好经过的中点,如图 , 其他条件不变,求的值.
(1)、求证:∽;(2)、求的度数;(3)、若正方形的边长为 , 点是延长线上一点,交的延长线于点 , 且恰好经过的中点,如图 , 其他条件不变,求的值.