贵州省遵义市红花岗区2023年中考三模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 当前,手机移动支付已经成为新型的消费方式,中国正在向无现金支付发展,若收入元记作元,则元记作( )A、收入元 B、支出元 C、收入元 D、支出元2. 把一个正五棱柱如图摆放,光线由上向下照射,此正五棱柱的正投影是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. “五一”假期,我市各大景区迎来旅游热潮遵义会议会址景区累计接待万人次,创“五一”假期历史接待人数新高将数据万用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,由 , 能得到的是( )A、
3. “五一”假期,我市各大景区迎来旅游热潮遵义会议会址景区累计接待万人次,创“五一”假期历史接待人数新高将数据万用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,由 , 能得到的是( )A、 B、
B、 C、
C、 D、
D、 5. 在平面直角坐标系中,点关于原点的对称点的坐标是( )A、 B、 C、 D、6. 在下列各式的计算中,正确的是( )A、 B、 C、 D、7. 如图,、、、是数轴上的点,那么在数轴上对应的点可能是( )
5. 在平面直角坐标系中,点关于原点的对称点的坐标是( )A、 B、 C、 D、6. 在下列各式的计算中,正确的是( )A、 B、 C、 D、7. 如图,、、、是数轴上的点,那么在数轴上对应的点可能是( ) A、点 B、点 C、点 D、点8. 如图,小明沿一个五边形的广场小道按的方向跑步健身,他每跑完一圈时,身体转过的角度之和是( )
A、点 B、点 C、点 D、点8. 如图,小明沿一个五边形的广场小道按的方向跑步健身,他每跑完一圈时,身体转过的角度之和是( ) A、 B、 C、 D、9. 一元二次方程的根是( )A、 , B、 , C、 , D、 ,10. 如图,点是线段上的动点不与点、重合 , 分别以、为边向上作等边三角形和 , 延长、交于点 , 若 , 则四边形的周长是( )
A、 B、 C、 D、9. 一元二次方程的根是( )A、 , B、 , C、 , D、 ,10. 如图,点是线段上的动点不与点、重合 , 分别以、为边向上作等边三角形和 , 延长、交于点 , 若 , 则四边形的周长是( ) A、 B、 C、 D、11. 甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差如图所示,根据图中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A、 B、 C、 D、11. 甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差如图所示,根据图中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( ) A、甲 B、乙 C、丙 D、丁12. 如图 , 是的直径,点、、将半圆分成四等分,把五位同学分别编为序号、、、、按顺序站在半圆的五个点上,现把最右边的号同学调出,站到号和号两位同学之间,再把最右边的号同学调出,站到号和号两位同学之间,得到图 , 称为“次换序”接着按同样的方法,把最右边的号同学调出,站到号和号两位同学之间,再把最右边的号同学调出,站到号和号两位同学之间,得到图 , 称为“次换序”以此类推,;若从图开始,经过“次换序”后,得到的顺序与图相同,则的值可以是( )
A、甲 B、乙 C、丙 D、丁12. 如图 , 是的直径,点、、将半圆分成四等分,把五位同学分别编为序号、、、、按顺序站在半圆的五个点上,现把最右边的号同学调出,站到号和号两位同学之间,再把最右边的号同学调出,站到号和号两位同学之间,得到图 , 称为“次换序”接着按同样的方法,把最右边的号同学调出,站到号和号两位同学之间,再把最右边的号同学调出,站到号和号两位同学之间,得到图 , 称为“次换序”以此类推,;若从图开始,经过“次换序”后,得到的顺序与图相同,则的值可以是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共16.0分)
-
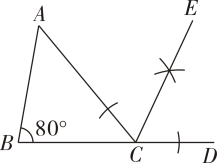
13. 化简: = .14. 已知 , , 则 .15. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .
 16. 如图,已知 , , , 以为斜边作 , 连接 , 作 , 若 , 且 , 则的长为 .
16. 如图,已知 , , , 以为斜边作 , 连接 , 作 , 若 , 且 , 则的长为 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算:;(2)、解分式方程: .18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于 , 两点,与轴交于点 .
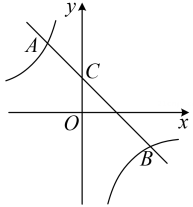 (1)、求这两个函数的解析式;(2)、求的面积.19. 年月日,中共中央办公厅、国务院办公厅印发关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见某校积极落实“双减”政策,准备开设拓展课程为了让学生可以根据自己的兴趣爱好选择最喜欢的课程,该校随机抽取了部分学生进行了问卷调查问卷设置以下四门课程:综合模型、摄影艺术、音乐鉴赏、劳动实践 , 要求每名学生必须选择并且只能选择其中最喜欢的一门课程,并将调查结果整理绘制成如下不完整的统计图.
(1)、求这两个函数的解析式;(2)、求的面积.19. 年月日,中共中央办公厅、国务院办公厅印发关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见某校积极落实“双减”政策,准备开设拓展课程为了让学生可以根据自己的兴趣爱好选择最喜欢的课程,该校随机抽取了部分学生进行了问卷调查问卷设置以下四门课程:综合模型、摄影艺术、音乐鉴赏、劳动实践 , 要求每名学生必须选择并且只能选择其中最喜欢的一门课程,并将调查结果整理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)、被调查的学生人数为 名,并直接在答题卡中补全条形统计图;(2)、求拓展课程劳动实践所对应的扇形的圆心角的度数;(3)、小明和小兰都从、、、四门课程中选择一门自己喜欢的课程,请用列表或画树状图的方法求他们选中同一门课程的概率.20. 如图,、、分别是各边的中点,连接、、 .
 (1)、求证:四边形为平行四边形;(2)、加上条件 后,能使得四边形为菱形请从下面三个条件中选择个条件填空写序号 , 并加以证明.
(1)、求证:四边形为平行四边形;(2)、加上条件 后,能使得四边形为菱形请从下面三个条件中选择个条件填空写序号 , 并加以证明.
;
平分;
.21. 在一次课外实践活动中,九年级数学兴趣小组准备测量校园内的一栋教学楼的高度,同学们设计了两个测量方案如下:课题
测量教学楼的高度
测量工具
测角仪,标杆,皮尺等
测量小组
第一小组
第二小组
测量方案示意图


说明
点、、在同一直线上,、为标杆
为教学楼旁边的两层小楼
测量数据
从点处测得点的仰角为 , 从点处测得点的仰角为 ,
从点处测得点的仰角为 ,
(1)、根据以上数据请你判断,第 小组无法测量出教学楼的高度?(2)、请根据表格中的数据,依据正确的测量方案求出教学楼的高度精确到 , 参考数据: , ,22. 如图,已知是的直径,弦于点 , 连接 , 将沿翻折得到 , 直线与直线相交于点 .
 (1)、求证:直线与相切;(2)、若 , 求阴影部分的面积.23. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵元,一盒猪肉粽加两盒豆沙粽进价为元.(1)、求每盒猪肉粽和豆沙粽的进价;
(1)、求证:直线与相切;(2)、若 , 求阴影部分的面积.23. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵元,一盒猪肉粽加两盒豆沙粽进价为元.(1)、求每盒猪肉粽和豆沙粽的进价;
(2)、在销售中,某商家发现当每盒猪肉粽售价为元时,每天可售出盒,若每盒售价提高元,则每天少售出盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.24. 定义:二次项系数之和为 , 对称轴相同,且图象与轴交点也相同的两个二次函数互为友好同轴二次函数例如:的友好同轴二次函数为 .(1)、函数的对称轴为 其友好同轴二次函数为 .(2)、已知二次函数:其中且且 , 其友好同轴二次函数记为 .
若函数的图象与函数的图象交于、两点点的横坐标小于点的横坐标 , 求线段的长;
当时,函数的最大值与最小值的差为 , 求的值.25. 【问题背景】如图 , 在中,将劣弧沿弦所在的直线折叠,使得劣弧恰好过圆心 , 圆心关于直线的对称点为 . (1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.
(1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.