贵州省贵阳市乌当区2023年中考模拟数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算的值是( )A、 B、 C、 D、2. 下列新能源汽车车标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某小组名学生的中考体育分数单位分如下: , , , , , , , , 则该组数据的众数、中位数分别为( )A、 , B、 , C、 , D、 ,4. 计算的结果为( )A、 B、 C、 D、5. 任意掷一枚质地均匀的骰子,正面朝上的点数为的概率是( )A、 B、 C、 D、6. 近年来,贵州省以“四好农村路”建设为契机,相继创新规划了六盘水市“一带两翼”、遵义市“一环九带”、铜仁市“一带四环”、黔南州“一路三带三环”、黔东南州“一路三带五环”等极具乡域特色的美丽农村路经济示范走廊达公里,其中这个数用科学记数法可表示为( )A、 B、 C、 D、7. 如图,在中,是的中点,连接 , 过作 , 交于 , 已知 , , 则的长是( )
3. 某小组名学生的中考体育分数单位分如下: , , , , , , , , 则该组数据的众数、中位数分别为( )A、 , B、 , C、 , D、 ,4. 计算的结果为( )A、 B、 C、 D、5. 任意掷一枚质地均匀的骰子,正面朝上的点数为的概率是( )A、 B、 C、 D、6. 近年来,贵州省以“四好农村路”建设为契机,相继创新规划了六盘水市“一带两翼”、遵义市“一环九带”、铜仁市“一带四环”、黔南州“一路三带三环”、黔东南州“一路三带五环”等极具乡域特色的美丽农村路经济示范走廊达公里,其中这个数用科学记数法可表示为( )A、 B、 C、 D、7. 如图,在中,是的中点,连接 , 过作 , 交于 , 已知 , , 则的长是( ) A、 B、 C、 D、8. 如图, 的顶点是正方形网格的格点,则 的值为( )
A、 B、 C、 D、8. 如图, 的顶点是正方形网格的格点,则 的值为( )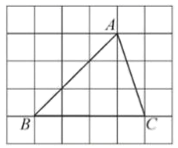 A、 B、 C、 D、9. 若一次函数的图经过点和 , 则的值是( )A、 B、 C、 D、10. 若菱形两条对角线和的长度是方程的两根,则该菱形的边长为( )
A、 B、 C、 D、9. 若一次函数的图经过点和 , 则的值是( )A、 B、 C、 D、10. 若菱形两条对角线和的长度是方程的两根,则该菱形的边长为( ) A、 B、 C、 D、11. 若分式的值为零,则的值为( )A、 B、 C、 D、以上均有可能12. 如图,在平面直角坐标系中,二次函数与轴交于 , , , 是方程的两个根,且 , 则下列不等式正确的是( )
A、 B、 C、 D、11. 若分式的值为零,则的值为( )A、 B、 C、 D、以上均有可能12. 如图,在平面直角坐标系中,二次函数与轴交于 , , , 是方程的两个根,且 , 则下列不等式正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共16.0分)
-
13. 在二次根式中,的取值范围是 .14. 已知二元一次方程 , 请写出该方程的一组整数解 .15. 如图,在中,点 , 分别是 , 的中点,若 , 则 .
 16. 如图,四边形的对角线和相交于点 , 若 , 且 , , , 则的长为 .
16. 如图,四边形的对角线和相交于点 , 若 , 且 , , , 则的长为 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、关于的不等式组解集在数轴上表示如图 , 请写出一个符合条件的不等式组: ;
 (2)、关于的不等式的解集在数轴上表示如图 , 则 ;
(2)、关于的不等式的解集在数轴上表示如图 , 则 ; (3)、解这个二元一次方程组 .18. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.19. 年月,教育部正式印发义务教育课程方案 , 劳动教育成为一门独立的课程,官渡区某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙墙的最大可用长度为米 , 用长为米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端各设计了两个宽米的小门,供同学们进行劳动实践,若设菜地的宽为米.
(3)、解这个二元一次方程组 .18. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.19. 年月,教育部正式印发义务教育课程方案 , 劳动教育成为一门独立的课程,官渡区某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙墙的最大可用长度为米 , 用长为米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端各设计了两个宽米的小门,供同学们进行劳动实践,若设菜地的宽为米.
 (1)、 米用含的代数式表示;(2)、若围成的菜地面积为平方米,求此时的宽 .20. 我校中学数学兴趣小组借助无人机测量一条河流的宽 , 如图所示,一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为 , 无人机的正东方向继续飞行米至处,测得正前方河流右岸处的俯角为 , 线段的长为无人机距地面的垂直高度,点、、在同一条直线上,其中 , 米
(1)、 米用含的代数式表示;(2)、若围成的菜地面积为平方米,求此时的宽 .20. 我校中学数学兴趣小组借助无人机测量一条河流的宽 , 如图所示,一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为 , 无人机的正东方向继续飞行米至处,测得正前方河流右岸处的俯角为 , 线段的长为无人机距地面的垂直高度,点、、在同一条直线上,其中 , 米
 (1)、求无人机的飞行高度结果保留根号
(1)、求无人机的飞行高度结果保留根号
(2)、求河流的宽度结果精确到米,参考数据: ,21. 如图,矩形中,点是中点,线段的延长线与的延长线交于点 .
 (1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 如图,在平面直角坐标系中,一次函数和反比例函数在第一象限内的图象交于点 .
(1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 如图,在平面直角坐标系中,一次函数和反比例函数在第一象限内的图象交于点 .
 (1)、求反比例函数的表达式;(2)、将一次函数图象向上平移后与反比例函数图象在第一象限内交于点 , 与轴交于点 , 且的面积为 , 求平移后的一次函数表达式.23. 如图,在中, , , 交点 , 为的直径, .
(1)、求反比例函数的表达式;(2)、将一次函数图象向上平移后与反比例函数图象在第一象限内交于点 , 与轴交于点 , 且的面积为 , 求平移后的一次函数表达式.23. 如图,在中, , , 交点 , 为的直径, .
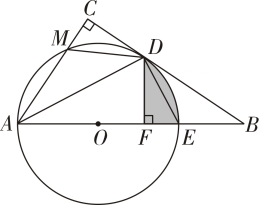 (1)、求证:;(2)、若平分 , 求的度数;(3)、若 , 求图中阴影部分的面积.24. 如图,在平面直角坐标系中,抛物线与轴交于点 , 与轴交于点 , 是该抛物线上一点,其横坐标为 , 过作轴的垂线,垂足为 , 作线段关于轴的对称段 , 连接得矩形 .
(1)、求证:;(2)、若平分 , 求的度数;(3)、若 , 求图中阴影部分的面积.24. 如图,在平面直角坐标系中,抛物线与轴交于点 , 与轴交于点 , 是该抛物线上一点,其横坐标为 , 过作轴的垂线,垂足为 , 作线段关于轴的对称段 , 连接得矩形 .
 (1)、求该抛物线对应的函数表达式;(2)、当点在矩形的边上时,求的值;(3)、当矩形的边与该抛物线有三个交点时,直接写出的取值范围.25. 已知正方形 , , 是对角线上任意一点.
(1)、求该抛物线对应的函数表达式;(2)、当点在矩形的边上时,求的值;(3)、当矩形的边与该抛物线有三个交点时,直接写出的取值范围.25. 已知正方形 , , 是对角线上任意一点. (1)、如图 , 以为边向右作等腰直角三角形 , , 连接 , 则和的数量关系是 ;(2)、如图 , 点在上, , , 求的长为多少;(3)、为上任意一点不与 , 重合 , 作于 , 连接 , 为上一点,且 , 当点从点运动到点时,写出点运动的路径的长.
(1)、如图 , 以为边向右作等腰直角三角形 , , 连接 , 则和的数量关系是 ;(2)、如图 , 点在上, , , 求的长为多少;(3)、为上任意一点不与 , 重合 , 作于 , 连接 , 为上一点,且 , 当点从点运动到点时,写出点运动的路径的长.