贵州省遵义市红花岗区2023年中考二模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在下列四个实数中，最小的数是（）

A、 $- 2$ B、 $0$ C、 $\sqrt{3}$ D、 $\frac{5}{3}$

查看试题解析
2. 2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯，历届世界杯可谓各具特色，会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 祖冲之发现的圆周率的分数近似值 $\frac{355}{113} \approx 3.1415929$ ，称为密率，比 $π$ 的值只大 $0.0000003$ ， $0.0000003$ 这个数用科学记数法可表示为（）

A、 $0.3 \times 1 0^{- 6}$ B、 $0.3 \times 1 0^{- 7}$ C、 $3 \times 1 0^{- 6}$ D、 $3 \times 1 0^{- 7}$

查看试题解析
4. 如图，利用工具测量角，则 $∠ 1$ 的大小为（）

A、 $30 °$ B、 $60 °$ C、 $40 °$ D、 $50 °$

查看试题解析
5. 下列计算正确的是（）

A、 $(- 2 a)^{3} = - 6 a^{3}$ B、 $4 a^{3} \cdot 3 a^{2} = 12 a^{5}$
C、 $- 8 a^{4} \div 4 a = - 2 a$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
6. 如图， $△ A B C$ 沿 $B C$ 方向平移后得到 $△ D E F$ ，已知 $B C = 7$ ， $E C = 2$ ，则平移的距离是（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

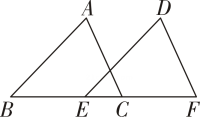查看试题解析
7. 九年级第一次体育模考中，某班有 $8$ 名同学选择了跳绳项目，他们的跳绳成绩如下： $($ 单位：个 $/$ 分 $) 177$ 、 $167$ 、 $171$ 、 $169$ 、 $164$ 、 $159$ 、 $166$ 、 $168$ ，则这组数据的中位数是（）

A、 $167$ B、 $168$ C、 $166.5$ D、 $167.5$

查看试题解析
8. 如图，小明家仿古家具的一块三角形形状的玻璃坏了，需要重新配一块．小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为 $△ A B C$ ，提供下列各组元素的数据，配出来的玻璃不一定符合要求的是（）

A、 $A B$ ， $B C$ ， $C A$ B、 $A B$ ， $B C$ ， $∠ B$ C、 $A B$ ， $A C$ ， $∠ B$ D、 $∠ A$ ， $∠ B$ ， $B C$

查看试题解析
9. 如图，直线 $l_{1}$ ： $y = k x$ 与直线 $l_{2}$ ： $y = m x - 3$ 交于点 $A (3 ， 2)$ ，则不等式 $m x - 3 < k x$ 的解集是（）

A、 $x > 2$ B、 $x < 2$ C、 $x > 3$ D、 $x < 3$

查看试题解析
10. 如图，在 $△ A B C$ 中，按以下步骤作图： $①$ 分别以 $B$ ， $C$ 为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于 $M$ ， $N$ 两点； $②$ 作直线 $M N$ 交 $A B$ 于点 $D$ ，连接 $C D .$ 若 $A D = A C$ ， $∠ A = 56 °$ ，则 $∠ A C B$ 的度数为（）

A、 $90 °$ B、 $93 °$ C、 $100 °$ D、 $112 °$

查看试题解析
11. 某校九年级 $1$ 班学生小聪家和小明家到学校的直线距离分别是 $7 k m$ 和 $5 k m .$ 那么小聪，小明两家的直线距离不可能是（）

A、 $1 k m$ B、 $2 k m$ C、 $5 k m$ D、 $12 k m$

查看试题解析
12. 对于两个不相等的实数 $a$ ， $b$ ，我们规定符号 $m a x (a ， b)$ 表示 $a$ ， $b$ 中的较大值，如： $m a x (3 ， 5) = 5$ ，因此， $m a x (- 3 ， - 5) = - 3$ ：按照这个规定，若 $m a x {x ， - x} = x^{2} - 3 x - 5$ ，则 $x$ 的值是（）

A、 $5$ B、 $5$ 或 $1 - \sqrt{6}$ C、 $- 1$ 或 $1 - \sqrt{6}$ D、 $5$ 或 $1 + \sqrt{6}$

查看试题解析

二、填空题（本大题共4小题，共16.0分）

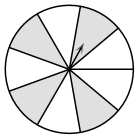
13. 若 $\sqrt{x - 5}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
14. 如图，一个可以自由转动的转盘，被分成了9个相同的扇形，转动转盘，转盘停止时，指针落在阴影区域的概率等于．

查看试题解析
15. 如图，冰淇淋蛋筒下部呈圆锥形，底面直径为 $6 c m$ ，母线长为 $10 c m$ ，则这个蛋筒圆锥部分包装纸的面积 $($ 接口忽略不计 $)$ 是 $c m^{2} . ($ 结果保留 $π)$

查看试题解析
16. 已知 $△ A B C$ 内接于 $⊙ O$ ，它的内心为点 $D$ ，连接 $A D$ 交弦 $B C$ 于点 $E$ ，交 $⊙ O$ 于点 $F$ ，已知 $B E = 5$ ， $C E = 4$ ， $E F = 3$ ，则线段 $D E$ 的长为．

查看试题解析

三、解答题（本大题共9小题，共98.0分。解答应写出文字说明，证明过程或演算步骤）

17.

(1)、计算： $- (- 2) - (- \frac{1}{2})^{- 2} + \sqrt{9}$ ；

(2)、解不等式组 ${\begin{array}{l} \frac{1}{2} x + 1 \geq - 1 \\ 1 - 2 x \geq 3 \end{array}$ ．

查看试题解析
18. 小红在计算 $(\frac{a}{a - b} - 1) \div \frac{b}{a^{2} - b^{2}}$ 时，解答过程如下：
原式 $= \frac{a - a - b}{a - b} \div \frac{b}{(a + b) (a - b)} ①$
$= \frac{- b}{a - b} \cdot \frac{(a + b) (a - b)}{b} ②$
$= - a - b ③$

(1)、小红的解答从第步开始出错；

(2)、请写出正确的解答过程．

查看试题解析
19. 近日遵义某中学为更好地落实“双减”政策，提高课后服务质量，对部分家长进行关于对学校课后服务质量满意度的问卷调查，在此次调查中对问卷选项做了数据分析，其中 $A$ 为非常满意、 $B$ 为比较满意、 $C$ 为一般、 $D$ 为不太满意 $.$ 并绘制了如下的两幅不完整的统计图，请根据图中的相关信息解决下列问题：

(1)、参与这次调查的学生家长共计人，扇形统计图中 $C$ 所对应扇形的圆心角的度数是；

(2)、将图中的统计图补充完整；

(3)、若该校学生共有 $900$ 名，请估计对课后服务比较满意和非常满意的家长共多少人？

查看试题解析
20. 如图，反比例函数 $y = \frac{8}{x}$ 的图象与一次函数图象 $y = k x - 5 (k$ 为常数，且 $k \neq 0)$ 的图象交于 $A$ 、 $B (- 2 ， m)$ 两点．

(1)、求一次函数的表达式；

(2)、若将直线 $A B$ 向上平移 $n (n > 0)$ 个单位长度后与反比例函数的图象有且只有一个公共点，求 $n$ 的值．

查看试题解析
21. 数学社团的同学运用自己所学的知识进行区间测速，他们将观测点设在距遵义大道 $50$ 米的点 $P$ 处，如图，直线 $l$ 表示遵义大道 $.$ 这时一辆小汽车由进义大道上的 $A$ 处向 $B$ 处匀速行驶，用时 $4$ 秒 $.$ 经测点 $A$ 在点 $P$ 的南偏西 $30 °$ 方向上，点 $B$ 在点 $P$ 的南偏西 $53 °$ 方向上．

(1)、求 $A$ 、 $B$ 之间的路程 $($ 精确到 $0.1$ 米 $)$ ；

(2)、请判断此车是否超过了遵义大道 $60$ 千米 $/$ 时的限制速度？ $($ 参考数据： $\sqrt{3} \approx 1.732$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75)$

查看试题解析
22. 为拓展学生视野，促进书本知识与生活实践的深度融合，某中学组织九年级全体学生前往某研学基地开展研学活动，在此次活动中，若每位老师带队 $15$ 名学生，则还剩 $10$ 名学生没老师带；若每位老师带队 $16$ 名学生，就有一位老师少带 $5$ 名学生 $.$ 学校计划此次研学活动共租 $8$ 辆车，租金总费用不超过 $3000$ 元 $.$ 现有甲、乙两种大型客车，它们的载客量和租金如下表所示：

甲型客车
乙型客车
载客量 $($ 人 $/$ 辆 $)$
          $35$
          $30$
租金 $($ 元 $/$ 辆 $)$
          $400$
          $320$

(1)、参加此次研学活动的老师和学生各有多少人？

(2)、学校共有几种租车方案？最少租车费用是多少？

查看试题解析
23. “抖空竹”在我国有着悠久的历史，是国家级的非物质文化遗产之一 $.$ 小亮玩”抖空竹”游戏时发现可以将某时刻的情形抽象成数学问题 $.$ 如图， $A C$ 、 $B D$ 分别与 $⊙ O$ 相切于点 $C$ 、 $D$ ，延长 $A C$ 、 $B D$ 交于点 $P$ ，连接 $O P$ 、 $C D$ ， $⊙ O$ 的半径为 $2$ ， $∠ D P C = 90 °$ ．

(1)、连接 $O C$ ， $O D$ ，判断四边形 $C O D P$ 的形状，并说明理由；

(2)、若某时刻 $∠ A P M = 60 °$ ， $P M$ 与 $C D$ 交于点 $N$ ，求 $P N$ 的长．

查看试题解析
24. 已知抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴相交于 $A$ 、 $B$ 两点，与 $y$ 轴相交于点 $C (0 ， 3)$ ， $A (- 3 ， 0)$ ．

(1)、求抛物线的解析式；

(2)、若点 $D$ 是线段 $A C$ 上方抛物线上的一个动点 $($ 点 $D$ 与 $A$ ， $C$ 不重合 $)$ ，求点 $D$ 到直线 $A C$ 的最大距离；

(3)、当 $t \leq x \leq t + 1$ 时，函数 $y = - x^{2} + b x + c$ 的最大值为 $- 5$ ，求 $t$ 的值．

查看试题解析
25. 数学课上，李老师提出了一个问题：在矩形 $A B C D$ 中， $A B = 9$ ， $A D = 12$ ，在 $A D$ 边上取一点 $M$ 使 $A M = 8$ ，将 $A M$ 绕点 $A$ 顺时针旋转 $α$ 度到 $A G$ ，以 $A G$ 为边作矩形 $A E F G ($ 如图 $1$ 所示 $)$ ， $A E = 6$ ，连接 $D G$ 、 $B E$ 交于点 $N$ ．

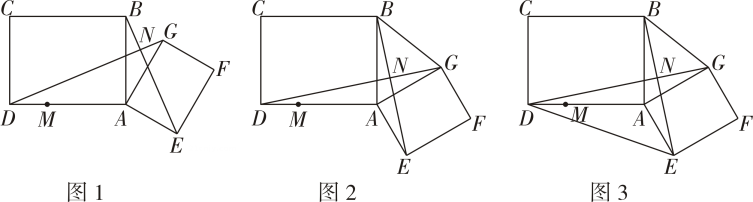(1)、求证： $D G ⊥ B E .$ 小明经过思考后，很快得到了解题思路：先用“两边对应成比例且夹角相等”证明 $△ A D G$ ∽ $△ A B E$ ，然后根据“直角三角形两锐角互余”可证明 $∠ B N D = ∠ B A D = 90 °$ ，从而得到 $D G ⊥ B E .$ 请你按照他的思路完成证明过程；

(2)、连接 $B G$ ，当旋转角 $α = 150$ 时 $($ 如图 $2)$ ，求 $\frac{S_{△ A B G}}{S_{△ A D G}}$ 的值；

(3)、连接 $D E ($ 如图 $3)$ ，当 $0 < α < 180 °$ 时，小明发现 $D E^{2} + B G^{2}$ 是一个定值，请求出这个值．

查看试题解析

	甲型客车	乙型客车
载客量 $($ 人 $/$ 辆 $)$	$35$	$30$
租金 $($ 元 $/$ 辆 $)$	$400$	$320$