贵州省贵阳市息烽县2023年中考模拟数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列各数中,负数是( )A、 B、 C、 D、2. 如图,用一个平行于长方体底面的平面截长方体,截面的形状是( )
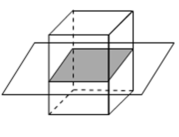 A、三角形
A、三角形
B、平行四边形
C、矩形
D、五边形3. 根据相关统计数据显示,年贵州省约为亿元,则这个数用科学记数法表示正确的是( )A、 B、 C、 D、4. 如图,直线 , 直线与被直线所截形成的几个角中,与相等的是( ) A、
A、
B、
C、
D、5. 已知 , 则的值是( )A、 B、 C、 D、6. 如图,在的网格中,其中有个小正方形被涂成了黑色,一个小球在此网格内自由滚动并随机地停留在某个小正方形上,它最终停留在黑色区域的概率是( )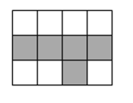 A、 B、 C、 D、7. 如图,是线段的垂直平分线,则下列结论一定正确的是( )
A、 B、 C、 D、7. 如图,是线段的垂直平分线,则下列结论一定正确的是( )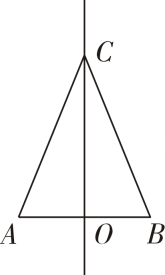 A、
A、
B、
C、
D、8. 若分式有意义,则的值不可能是( )A、 B、 C、 D、9. 如图是一张矩形纸片 , , 若将纸片沿折叠,使落在上,点的对应点为点 , 若 , 则( )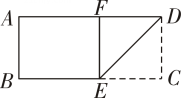 A、 B、 C、 D、10. 已知点的坐标为 , 则点关于轴对称的点为( )A、 B、 C、 D、11. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;作射线交于点 , 过点作于点 , 则下列结论不一定正确的是( )
A、 B、 C、 D、10. 已知点的坐标为 , 则点关于轴对称的点为( )A、 B、 C、 D、11. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;作射线交于点 , 过点作于点 , 则下列结论不一定正确的是( )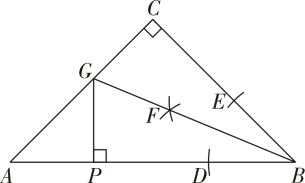 A、 B、
A、 B、
C、 D、12. 如图,两块完全重合的正方形纸片,如果上面的一块绕正方形的中心做的旋转,那么旋转时露出的的面积随着旋转角度的变化而变化,下面表示与关系的图象大致是( ) A、
A、 B、
B、
C、 D、
D、
二、填空题(本大题共4小题,共16.0分)
-
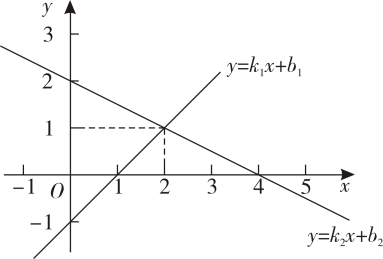
13. 已知是方程的根,则的值为 .14. 一个不透明的袋子中装有个不同颜色的球除颜色外其余相同 , 通过大量的摸球试验发现,摸到红球的概率稳定在 , 则据此估算袋中红球的个数是 .15. 在平面直角坐标系内,一次函数与为常数的图象如图所示,则关于的不等式的解集为 .
 16. 如图, , 分别是边长为的等边三角形的两边 , 上的动点,且 , 与交于点 , 则点到点的最小值为 .
16. 如图, , 分别是边长为的等边三角形的两边 , 上的动点,且 , 与交于点 , 则点到点的最小值为 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、先化解,再求值.
, 其中 , .(2)、在下列方程中选择两个你喜欢的方程,组成二元一次方程组,并进行解答.
;
;
.18. 贵阳市某初中开展了“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,学校采用了适当的调查方式并根据调查的结果绘制成如下统计图,请解答下列问题: (1)、本次调查应采用 填“普查”或“抽样调查”;(2)、扇形统计图中“排球”对应的值为 ,扇形的圆心角度数是 ;(3)、学校准备推荐甲、乙、丙、丁四名同学中的名参加全市中学生篮球比赛,请用列表法或画树状图法分析甲和乙同学同时被选中的概率.19. 如图,在▱中,对角线、交于点 , 分别延长、至点、点 , 且 , 连接 , , , .
(1)、本次调查应采用 填“普查”或“抽样调查”;(2)、扇形统计图中“排球”对应的值为 ,扇形的圆心角度数是 ;(3)、学校准备推荐甲、乙、丙、丁四名同学中的名参加全市中学生篮球比赛,请用列表法或画树状图法分析甲和乙同学同时被选中的概率.19. 如图,在▱中,对角线、交于点 , 分别延长、至点、点 , 且 , 连接 , , , . (1)、求证:;(2)、若 , 判断四边形的形状,并说出理由.20. 疫情期间,根据疫情防控需要,某校购进普通口罩和两种口罩共计个,购进普通口罩花费元,口罩花费元,其中口罩的价格是普通口罩价格的三倍,求两种口罩的单价.21. 如图,一次函数与反比例函数的图象相交于点 .
(1)、求证:;(2)、若 , 判断四边形的形状,并说出理由.20. 疫情期间,根据疫情防控需要,某校购进普通口罩和两种口罩共计个,购进普通口罩花费元,口罩花费元,其中口罩的价格是普通口罩价格的三倍,求两种口罩的单价.21. 如图,一次函数与反比例函数的图象相交于点 . (1)、求反比例函数的表达式;
(1)、求反比例函数的表达式;
(2)、是一次函数与轴的交点,过点作轴,垂足为 , 求的面积.22. 明明在家用新买的台灯做作业时,将台灯垂直放置于桌面,发现台灯可以抽象成如图所示的几何图形,于是使用工具量出了如下数据:到桌面的距离为 , , 请你求出台灯上的点到桌面的距离结果精确到 , 参考数据: , , , , , 23. 如图,在三角形中,点在上,以为半径的圆与相切于点 , 与相交于点 .
23. 如图,在三角形中,点在上,以为半径的圆与相切于点 , 与相交于点 . (1)、连接 , 若 , , 求的半径;(2)、连接 , 求证:;(3)、求证: .24. 某商品的进价是每件元,原售价每件元,进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:
(1)、连接 , 若 , , 求的半径;(2)、连接 , 求证:;(3)、求证: .24. 某商品的进价是每件元,原售价每件元,进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:售价元件
利润元
已知:利润售价进价销售量
(1)、当售价为每件元时,求当天售出多少件商品;
(2)、通过分析表格数据发现,该商品售价每件涨价元时,销售量减少件,设该商品上涨元,销售量为件,用所学过的函数知识求出与之间满足的函数表达式;
(3)、因当地物价局规定,该商品的售价不能超过进价的 , 请求出该商品利润与之间的函数关系式,并计算售价为多少元时,该商品获得最大利润.25. 在学习等腰直角三角形中,发现了很多有趣的问题.
 (1)、问题解决:如图 , 为等腰直角三角形上一点,绕点逆时针旋转得 , 连接 , 求证:;(2)、问题探究:如图 , 在的条件下,连接 , 探究 , , 之间的数量关系;(3)、拓展延伸:如图 , 在四边形中, , , 连接 , 则 , , 之间有怎样的数量关系,并证明你的结论.
(1)、问题解决:如图 , 为等腰直角三角形上一点,绕点逆时针旋转得 , 连接 , 求证:;(2)、问题探究:如图 , 在的条件下,连接 , 探究 , , 之间的数量关系;(3)、拓展延伸:如图 , 在四边形中, , , 连接 , 则 , , 之间有怎样的数量关系,并证明你的结论.