贵州省贵阳市白云区2023年中考模拟数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列各数是正数的是（）

A、 $5$ B、 $0$ C、 $- 1$ D、 $- \sqrt{2}$

查看试题解析
2. 如图，用一个平面去截一个正方体，截去的几何体是一个三棱锥，截面的形状是（）

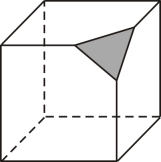A、六边形
B、圆
C、正方形
D、三角形

查看试题解析
3. 从贵阳市文化和旅游局获悉，“五一”假日期间，黔灵山公园接待游客量创历史新高，约为 $460000$ 人次， $460000$ 这个数用科学记数法可表示为（）

A、 $0.46 \times 1 0^{6}$ B、 $4.6 \times 1 0^{5}$ C、 $4.6 \times 1 0^{4}$ D、 $46 \times 1 0^{4}$

查看试题解析
4. 小颖、小明两人做游戏，掷一枚硬币，双方约定：正面朝上小颖胜，反面朝上小明胜，则这个游戏（）

A、公平 B、对小颖有利 C、对小明有利 D、无法确定

查看试题解析
5. 下列选项中，最简二次根式是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{7}$ D、 $\sqrt{9}$

查看试题解析
6. 下列各数中，能使不等式 $x - 1 \geq 2$ 成立的 $x$ 的整数值是（）

A、 $- 1$ B、 $0$ C、 $2$ D、 $3$

查看试题解析
7. 一名射击爱好者 $7$ 次射击成绩 $($ 单位：环 $)$ 依次为： $6$ ， $10$ ， $7$ ， $9$ ， $8$ ， $9$ ， $5$ ，去掉一个最高成绩和一个最低成绩后 $.$ 下列数据一定不发生变化的是（）

A、方差 B、中位数 C、众数 D、平均数

查看试题解析
8. 如图， $8 \times 8$ 的正方形网格中， $△ A B C$ 和 $△ E D C$ 的顶点都在正方形网格的格点处，则 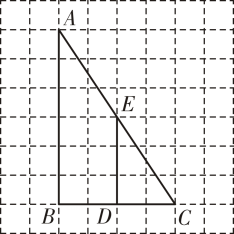$△ A B C$ 和 $△ E D C$ 的周长比是（）

A、 $\sqrt{2} ： 1$
B、 $2$ ： $1$
C、 $4$ ： $1$
D、 $5$ ： $2$

查看试题解析
9. 如图，在平面直角坐标系中，菱形 $O A B C$ 的顶点 $O$ ， $B$ 的坐标分别是 $(0 ， 0)$ ， $(4 ， 0)$ ， $∠ A = 60 °$ ，则顶点 $C$ 的坐标是（）

A、 $(2 ， 1)$
B、 $(2 ， - 1)$
C、 $(2 ， - \frac{2 \sqrt{3}}{3})$
D、 $(2 ， - 2 \sqrt{3})$

查看试题解析
10. 为鼓励学生积极参加阳光体育健身活动，某学校计划购买一批篮球和足球 $.$ 若购买 $30$ 个篮球， $20$ 个足球，需花费 $2350$ 元；若购买 $20$ 个篮球， $40$ 个足球，需花费 $2500$ 元 $.$ 则篮球、足球的单价各是多少元？设篮球的单价为 $x$ 元，足球的单价为 $y$ 元，则下列方程组正确的是（）

A、 ${\begin{array}{l} 30 x + 20 y = 2500 \\ 20 x + 40 y = 2350 \end{array}$ B、 ${\begin{array}{l} 30 x + 20 y = 2350 \\ 20 x + 40 y = 2500 \end{array}$
C、 ${\begin{array}{l} 20 x + 30 y = 2500 \\ 40 x + 20 y = 2350 \end{array}$ D、 ${\begin{array}{l} 20 x + 30 y = 2350 \\ 40 x + 20 y = 2500 \end{array}$

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ C A B = 65 °$ ，将 $△ A B C$ 在平面内绕点 $A$ 旋转到 $△ A B' C'$ 的位置，使 $C C' / / A B$ ，则旋转角的度数为（）

A、 $35 °$
B、 $40 °$
C、 $50 °$
D、 $65 °$

查看试题解析
12. 已知，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = \frac{1}{2} x$ 的图象向下平移 $1$ 个单位长度得到 $.$ 当 $x > - 2$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值都大于一次函数 $y = k x + b$ 的值，则 $m$ 的取值范围是（）

A、 $m \leq - 2$ B、 $m \geq \frac{1}{2}$ C、 $- 1 \leq m \leq \frac{1}{2}$ D、 $\frac{1}{2} \leq m \leq 1$

查看试题解析

二、填空题（本大题共4小题，共16.0分）

13. 已知 $x^{2} - y^{2} = 10$ ， $x - y = 2$ ，则 $x + y$ 等于．

查看试题解析
14. 当 $k =$ ，反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(\sqrt{2} ， - 2)$ ．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线交 $A C$ 于点 $D$ ，交 $A B$ 于点 $E .$ 若 $A E = 5$ ， $△ C B D$ 的周长为 $18$ ，则 $△ A B C$ 的周长为．

查看试题解析
16. 如图，在边长为 $2$ 的正六边形 $A B C D E F$ 中，点 $M$ ， $N$ 分别是 $A F$ ， $C D$ 的中点，连接 $B N$ ， $C M$ ， $B N$ 与 $C M$ 相交于点 $P$ ，则 $\frac{B P}{P N}$ 的值为．

查看试题解析

三、解答题（本大题共9小题，共98.0分。解答应写出文字说明，证明过程或演算步骤）

17.

(1)、当 $m =$ ，关于 $x$ 的方程 $(m - 1) x^{2} + 2 x - 6 = 0$ 是一元一次方程；

(2)、解一元二次方程 $x^{2} + 2 x - 6 = 0$ ．

查看试题解析

18. 根据国家统计局、国家能源局、中电联等机构的公开数据，整理

2022

年全国各类发电量数据后

.

绘制出各类发电量的统计表和统计图如表：

发电类型	发电量 $($ 万亿 $k W h)$
燃煤	$a$
水电	$1.355$
太阳能	$0.428$
风力	$0.762$
燃气	$0.269$
核电	$0.418$
生物质	$0.184$
其他	$0.2$

(1)、

2022

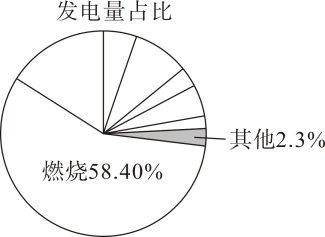年全国各类发电量的类型中，发电量最少的是，发电量为万亿

k W h

；

(2)、

2022

年全国各类发电量总量约为万亿

k W h

，表格中

a =

万亿

k W h

；

(

结果保留两位小数

)

(3)、节约用电，是我们每个人的责任和义务，我们应该时刻提醒自己和身边的人要节约用电，请对如何节约用电提一条合理化建议．

查看试题解析

19. 如图，四边形 $A B C D$ 是矩形，点 $E$ ， $F$ 分别是 $A B$ ， $C D$ 的中点，连接 $D E$ ， $B F$ ．

(1)、求证： $△ A D E$ ≌ $△ C B F$ ；

(2)、若 $∠ A D E = 45 °$ ， $A D = 6$ ，求四边形 $D F B E$ 的面积．

查看试题解析
20. 电商崛起，包裹量激增，人工分拣包裹速度已不能满足行业需求，为提高包裹的分拣速度，某公司引入智能机器人分拣系统，机器人分拣包裹速度是人工分拣包裹速度的 $5$ 倍，用机器人和人工分别分拣 $10000$ 件包裹，机器人所用时间比人工所用时间快 $8$ 小时，求机器人与人工分拣包裹的速度分别是每小时多少件？

查看试题解析
21. 如图，图 $①$ 是山坡顶上的信号塔，图 $②$ 是数学活动课上小红测量山高时使用的简图，已知信号塔高 $A C = 30 m$ ，使用测倾器在山脚下点 $B$ 处测得信号塔底 $C$ 的仰角为 $45 °$ ，塔顶 $A$ 的仰角为 $56 °$ ，求山高 $C D ($ 点 $A$ ， $C$ ， $D$ 在同一条竖直线上，点 $B$ ， $D$ 在同一条水平线上 $)$ ， $($ 结果保留 $1 m$ ，参考数据： $t a n 56 ° \approx 1.48$ ， $s i n 56 ° \approx 0.83$ ， $c o s 56 ° \approx 0.56)$

查看试题解析

22. 【建模】春节联欢晚会，九年级生活委员小星先购买了

2

个装饰挂件，共计

3

元，又购买了单价为

2

元的纸杯蛋糕

x

个，设所有装饰挂件和纸杯蛋糕的平均价格为

y

元，则

y

与

x

的关系式为

y = \frac{2 x + 3}{x + 2}

．
【探究】根据函数的概念，小星发现：

y

是

x

的函数，结合自己学习函数的经验，为了更好地研究这个函数，小星打算先脱离实际背景，对该函数的完整图象与性质展开探究，请根据所给信息，将探究过程补充完整

.

列表：

$x$	$\dots$	$- 5$	$- 4$	$- 3$	$- \frac{5}{2}$	$- \frac{3}{2}$	$- 1$	$0$	$1$	$2$	$\dots$
$y$	$\dots$	$\frac{7}{3}$	$\frac{5}{2}$	$m$	$4$	$n$	$1$	$\frac{3}{2}$	$\frac{5}{3}$	$\frac{7}{4}$	$\dots$

(1)、填空：

m =

，

n =

；

(2)、根据函数图象，写出一条该函数的性质；

(3)、【应用】根据上述探究，结合实际经验，小星得到结论：纸杯蛋糕个数越多，所购买物品的平均价格越，

(

填“高”或“低”

)

，但不会超过元

.

查看试题解析

23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，交 $B C$ 于点 $D$ ，点 $O$ 在 $A B$ 上， $⊙ O$ 经过 $A$ 、 $D$ 两点，交 $A C$ 于点 $E$ ，交 $A B$ 于点 $F$ ．

(1)、求证： $B C$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径是 $2 c m$ ， $E$ 是 $\overset{⏜}{A D}$ 的中点，求阴影部分的面积 $($ 结果保留 $π$ 和根号 $)$

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 4 a x + 1$ 与 $y$ 轴交于点 $A$ ，点 $B$ 与点 $A$ 关于该抛物线的对称轴对称，顶点为点 $C$ ．

(1)、写出二次函数的对称轴及点 $B$ 的坐标；

(2)、当 $△ A B C$ 的面积为 $3$ 时，求 $a$ 的值；

(3)、如图，点 $P (1 ， 0)$ ， $M (1 ， - 3)$ ， $N (4 ， - 3)$ ，当抛物线 $y = a x^{2} - 4 a x + 1$ 与 $△ P M N$ 的边只有 $2$ 个公共点时，求 $a$ 的取值范围．

查看试题解析
25. 如图，在边长为 $m$ 的正方形 $A B C D$ 中，点 $E$ ， $F$ 分别为 $C D$ ， $A B$ 边上的点，将正方形 $A B C D$ 沿 $E F$ 翻折，点 $B$ 的对应点为 $H$ ，点 $C$ 恰好落在 $A D$ 边的点 $G$ 处．

(1)、【问题解决】如图 $①$ ，连接 $C G$ ，则 $C G$ 与折痕 $E F$ 的位置关系是， $C G$ 与 $E F$ 的数量关系是；

(2)、【问题探究】如图 $②$ ，连接 $C H$ ，在翻折过程中， $G C$ 平分 $∠ D G H$ ，试探究 $△ C G H$ 的面积是否为定值，若为定值，请求出 $△ C G H$ 的面积；若不是定值，请说明理由；

(3)、【拓展延伸】若 $m = 3$ ，求出 $C H + C G$ 的最小值．

查看试题解析