贵州省铜仁市2023年中考三模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如果规定收入为正,支出为负,收入元记作 , 那么支出元记作( )A、元 B、元 C、元 D、元2. 截止年底,贵州省的常住人口约为人把“”用科学记数法表示为( )A、 B、 C、 D、3. 如图,直线 , 相交, , 则( )
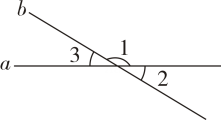 A、
A、
B、
C、
D、4. 下列计算,正确的是( )A、 B、
C、 D、5. 下列几何体中,主视图是长方形的为( )A、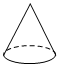 B、
B、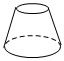 C、
C、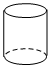 D、
D、 6. 如图,实数在数轴上的大致位置是( )
6. 如图,实数在数轴上的大致位置是( )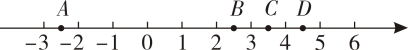 A、点 B、点 C、点 D、点7. 从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,S丙2=3.5,S丁2=3.68,你认为派谁去参赛更合适( )A、甲 B、乙 C、丙 D、丁8. 下列哪个是一元二次方程的解( )A、或 B、 C、或 D、无解9. 如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于 CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为( )
A、点 B、点 C、点 D、点7. 从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,S丙2=3.5,S丁2=3.68,你认为派谁去参赛更合适( )A、甲 B、乙 C、丙 D、丁8. 下列哪个是一元二次方程的解( )A、或 B、 C、或 D、无解9. 如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于 CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为( )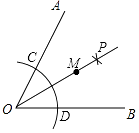 A、6 B、2 C、3 D、10. 在如图所示的直角坐标系中,的面积为 , 三个顶点的坐标分别为 , , , 、均为负整数,在图中的网格中,满足条件的点坐标有 ( )
A、6 B、2 C、3 D、10. 在如图所示的直角坐标系中,的面积为 , 三个顶点的坐标分别为 , , , 、均为负整数,在图中的网格中,满足条件的点坐标有 ( ) A、个 B、个 C、个 D、个11. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、
A、个 B、个 C、个 D、个11. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、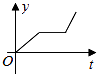 B、
B、 C、
C、 D、
D、 12. 如图,在平面直角坐标系网格中,点Q、R、S、T都在格点上,过点P(1,2)的抛物线y=ax2+2ax+c(a<0)可能还经过( )
12. 如图,在平面直角坐标系网格中,点Q、R、S、T都在格点上,过点P(1,2)的抛物线y=ax2+2ax+c(a<0)可能还经过( ) A、点Q B、点R C、点S D、点T
A、点Q B、点R C、点S D、点T二、填空题(本大题共4小题,共16.0分)
-
13. 计算: .14. 老师从甲、乙,丙、丁四位同学中任选一人去学校劳动基地浇水,选中甲同学的概率是 .15. 如图,菱形中, , 则 .
 16. 如图, 是等腰三角形, 过原点O,底边 轴双曲线 过A,B两点,过点C作 轴交双曲线于点D,若 ,则k的值是.
16. 如图, 是等腰三角形, 过原点O,底边 轴双曲线 过A,B两点,过点C作 轴交双曲线于点D,若 ,则k的值是.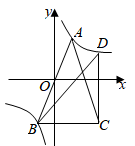
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算:;(2)、以下是欣欣解方程:的解答过程:
解:去分母,得;
去括号:;
移项,合并同类项得:;
解得:
欣欣的解答过程在第 步开始出错?请你完成正确的解答过程.18. 在某文具用品商店购买3个篮球和1个足球共花费190元;购买2个篮球和3个足球共花费220元.(1)、求购买1个篮球和1个足球各需多少元?(2)、若计划用不超过900元购买篮球和足球共20个,那么最多可以购买多少个篮球?19. 学期即将结束,王老师对自己任教的两个班每个班均为人的数学成绩进行质量检测,并对成绩进行统计,得出相关统计表和统计图.其中,成绩均为整数,满分分,成绩等级分为:优秀分及以上 , 良好分 , 合格分 , 不合格分以下班中良好这一组学生的成绩分别是: , , , , , , , , , .班成绩数据
平均数
众数
中位数
优秀率
人数
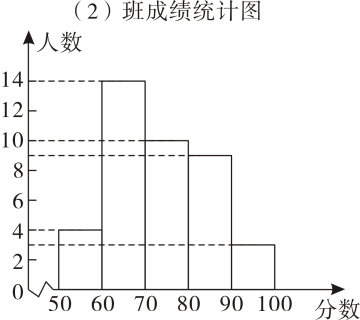
根据以上信息,回答下列问题,
(1)、写出班良好这一组成绩的中位数和众数;(2)、已知班没有人的成绩相同,则成绩是分的学生,在哪个班的名次更好些?请说明理由;(3)、根据上述信息,推断 班整体成绩更好,并从两个不同角度说明推断的合理性.20. 如图,在等腰直角三角形和中, , 点在边上,与交于点 , 连接 .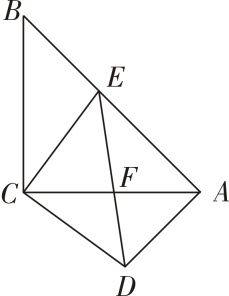 (1)、求证:≌ .
(1)、求证:≌ .
(2)、求证: .21. 如图所示,体育场内一看台与地面所成夹角为 , 看台最低点到最高点的距离米, , 两点正前方有垂直于地面的旗杆 , 在 , 两点处用仪器测量旗杆顶端的仰角分别为和结果精确到米 .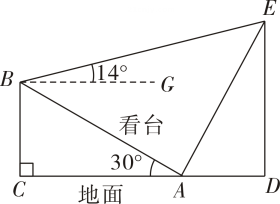 (1)、求的长;(2)、求旗杆的高22. 如图,为的直径,为的延长线上一点,过点作的切线,切点为点 , 连接、 , 过点作交延长线于点 .
(1)、求的长;(2)、求旗杆的高22. 如图,为的直径,为的延长线上一点,过点作的切线,切点为点 , 连接、 , 过点作交延长线于点 . (1)、求证: .(2)、若 , , 求的长.23. 如图,在平面直角坐标系中,直线与函数的图象交于点 , 与轴交于点 .
(1)、求证: .(2)、若 , , 求的长.23. 如图,在平面直角坐标系中,直线与函数的图象交于点 , 与轴交于点 .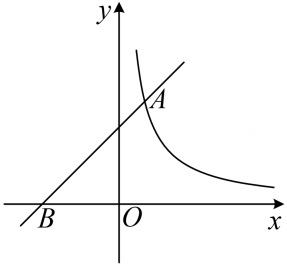 (1)、求 , 的值;(2)、过动点作平行于轴的直线,交函数的图象于点 , 交直线于点当时,求线段的长;(3)、在的条件下,若 , 结合函数的图象,直接写出的取值范围.24. 如图,抛物线与x轴交于点 , , 点A在点B的右侧,与y轴交于点C.
(1)、求 , 的值;(2)、过动点作平行于轴的直线,交函数的图象于点 , 交直线于点当时,求线段的长;(3)、在的条件下,若 , 结合函数的图象,直接写出的取值范围.24. 如图,抛物线与x轴交于点 , , 点A在点B的右侧,与y轴交于点C.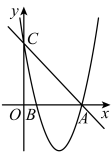 (1)、若直线AC的解析式为 , 求抛物线的解析式;(2)、在(1)的条件下,过点B的直线与抛物线交于另一点P.若直线AC与直线BP平行,求点P的坐标;(3)、点 , 为平面直角坐标系内两点,连结MN.若抛物线与线段MN只有一个公共点,直接写出c的取值范围.25. 中, , , 点为直线上一动点点不与 , 重合 , 以为边在右侧作菱形 , 使 , 连接 .
(1)、若直线AC的解析式为 , 求抛物线的解析式;(2)、在(1)的条件下,过点B的直线与抛物线交于另一点P.若直线AC与直线BP平行,求点P的坐标;(3)、点 , 为平面直角坐标系内两点,连结MN.若抛物线与线段MN只有一个公共点,直接写出c的取值范围.25. 中, , , 点为直线上一动点点不与 , 重合 , 以为边在右侧作菱形 , 使 , 连接 .
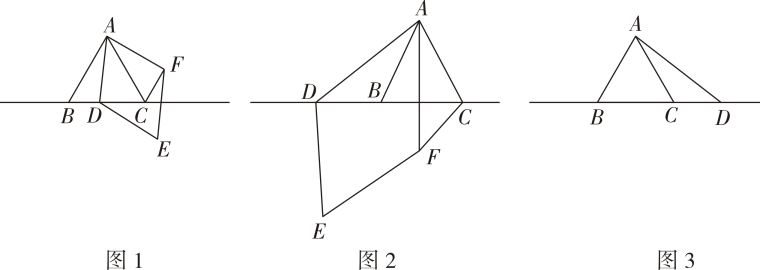 (1)、观察猜想:如图 , 当点在线段上时,
(1)、观察猜想:如图 , 当点在线段上时,
与的位置关系为: .
, , 之间的数量关系为:;(2)、数学思考:如图 , 当点在线段的延长线上时,结论 , 是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)、拓展延伸:如图 , 当点在线段的延长线上时,设与相交于点 , 若已知 , , 求的长.