贵州省遵义五十七中2023年中考四模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的倒数是( )A、 B、 C、 D、2. 计算正确的结果是( )A、 B、 C、 D、3. 在一个不透明的盒子中,装有质地、大小完全相同的白色乒乓球个,黄色乒乓球个随机摸出个球,摸到黄色乒乓球的概率是( )A、 B、 C、 D、4. 计算的结果为( )A、 B、 C、 D、5. 如图,在中,是边上的点, , :: , 则与的面积比是( )
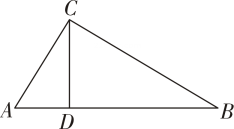 A、:
A、:
B、:
C、:
D、:6. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是( )A、5 cm B、10cm C、6cm D、5cm7. 新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,年销量为万辆,销量逐年增加,到年销量为万辆.设年平均增长率为 , 可列方程为( )A、 B、
C、 D、8. 如图所示,直线:与直线:交于点 , 不等式的解集是( ) A、
A、
B、
C、
D、9. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )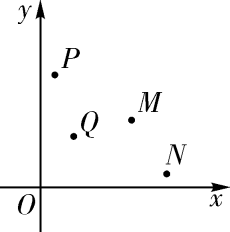 A、点 B、点 C、点 D、点10. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )
A、点 B、点 C、点 D、点10. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )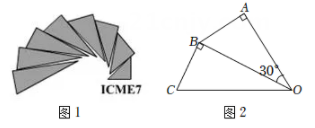 A、 B、 C、1 D、211. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列个结论:
A、 B、 C、1 D、211. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列个结论: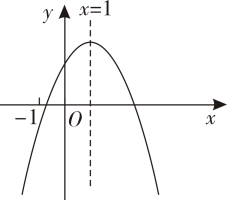
;;;; .
其中正确的结论有( )A、个
B、个
C、个
D、个12. 如图,在正方形中,和交于点 , 过点的直线交于点不与 , 重合 , 交于点以点为圆心,为半径的圆交直线于点 , 若 , 则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共16.0分)
-
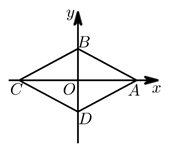
13. 在实数范围内分解因式: .14. 如图,在平面直角坐标系中,菱形 对角线的交点坐标是 ,点 的坐标是 ,且 ,则点 的坐标是.
 15. 如图,在四边形中,对角线 , 相交于点 , , .若 , 则的面积是 , 度.
15. 如图,在四边形中,对角线 , 相交于点 , , .若 , 则的面积是 , 度. 16. 如图,在等腰直角三角形中, , 点M,N分别为 , 上的动点,且 , .当的值最小时,的长为.
16. 如图,在等腰直角三角形中, , 点M,N分别为 , 上的动点,且 , .当的值最小时,的长为.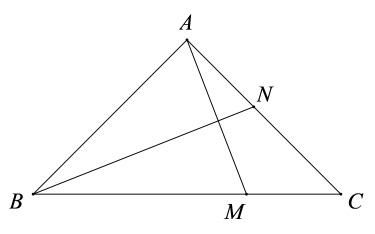
三、计算题
-
17.(1)、有三个不等式 , , , 请在其中任选两个不等式,组成一个不等式组,并求出它的解集;
(2)、小红在计算时,解答过程如下:第一步
第二步
第三步小红的解答从第 步开始出错,请写出正确的解答过程.
四、解答题(本大题共8小题,共88.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形两个转盘除表面数字不同外,其它完全相同 , 转盘甲上的数字分别是 , , , 转盘乙上的数字分别是 , , 规定:指针恰好停留在分界线上,则重新转一次 .
 (1)、转动转盘,转盘甲指针指向正数的概率是;转盘乙指针指向正数的概率是 .
(1)、转动转盘,转盘甲指针指向正数的概率是;转盘乙指针指向正数的概率是 .
(2)、若同时转动两个转盘,转盘甲指针所指的数字记为 , 转盘乙指针所指的数字记为 , 请用列表法或树状图法求满足的概率.19. 一次函数的图象与反比例函数的图象相交于 , 两点. (1)、求这个反比例函数的表达式;(2)、根据图象写出使一次函数值小于反比例函数值的的取值范围.20. 如图,在矩形 中,点 在 上, ,且 ,垂足为 .
(1)、求这个反比例函数的表达式;(2)、根据图象写出使一次函数值小于反比例函数值的的取值范围.20. 如图,在矩形 中,点 在 上, ,且 ,垂足为 . (1)、求证: ;(2)、若 ,求四边形 的面积.21. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
(1)、求证: ;(2)、若 ,求四边形 的面积.21. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题: (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).22. 如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).22. 如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC. (1)、求证:△ADB≌△BCA;(2)、若OD⊥AC,AB=4,求弦AC的长;(3)、在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.23. 遵义市开展信息技术与教学深度融合的精准化教学某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高20%,用30000元购买A型设备的数量比用15000元购买B型设备的数量多4台.(1)、求A,B型设备单价分别是多少元?(2)、该校计划购买两种设备共50台,要求A型设备数量不少于B型设备数量的.设购买a台A型设备,购买总费用为w元,求w与a的函数关系式,并求出最少购买费用.24. 如图,抛物线 : 与抛物线 : 开口大小相同、方向相反,它们相交于 , 两点,且分别与 轴的正半轴交于点 ,点 , .
(1)、求证:△ADB≌△BCA;(2)、若OD⊥AC,AB=4,求弦AC的长;(3)、在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.23. 遵义市开展信息技术与教学深度融合的精准化教学某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高20%,用30000元购买A型设备的数量比用15000元购买B型设备的数量多4台.(1)、求A,B型设备单价分别是多少元?(2)、该校计划购买两种设备共50台,要求A型设备数量不少于B型设备数量的.设购买a台A型设备,购买总费用为w元,求w与a的函数关系式,并求出最少购买费用.24. 如图,抛物线 : 与抛物线 : 开口大小相同、方向相反,它们相交于 , 两点,且分别与 轴的正半轴交于点 ,点 , .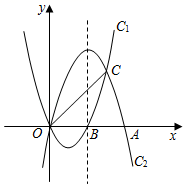 (1)、求抛物线 的解析式;(2)、在抛物线 的对称轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由;(3)、 是直线 上方抛物线 上的一个动点,连接 , , 运动到什么位置时, 面积最大?并求出最大面积.25. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
(1)、求抛物线 的解析式;(2)、在抛物线 的对称轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由;(3)、 是直线 上方抛物线 上的一个动点,连接 , , 运动到什么位置时, 面积最大?并求出最大面积.25. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .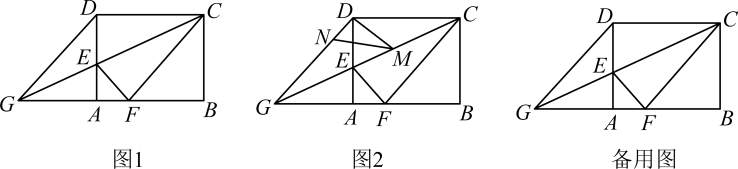 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
-