贵州省贵阳市白云区2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 中国是最早采用正负数表示相反意义量的国家,如果把收入元记作元,那么支出元记作( )A、元 B、元 C、元 D、元2. 如图,在平面内,直角三角板直角顶点落在直线上,已知 , 则的度数是( )
 A、 B、 C、 D、3. 中国天眼位于贵州省平塘县,其综合观测性能世界第一,它的内球面反射面积为平方米,相当于个
A、 B、 C、 D、3. 中国天眼位于贵州省平塘县,其综合观测性能世界第一,它的内球面反射面积为平方米,相当于个
足球场的面积,这个数用科学记数法可表示为( )A、 B、 C、 D、4. 如图,点P是直线l外一点,且 , 点C是垂足.点A,B,D在直线l上,下列线段中最短的是( ) A、 B、 C、 D、5. 在平面直角坐标系中,下列函数的图象经过原点的是( )A、 B、 C、 D、6. 如图所示,圆锥的左视图是( )A、
A、 B、 C、 D、5. 在平面直角坐标系中,下列函数的图象经过原点的是( )A、 B、 C、 D、6. 如图所示,圆锥的左视图是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在数轴上,以原点为圆心,的长为半径画弧,交数轴正半轴于点 , 则点对应的数是( )
7. 如图,在数轴上,以原点为圆心,的长为半径画弧,交数轴正半轴于点 , 则点对应的数是( ) A、 B、 C、 D、8. 若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、9. 化简的结果是( )A、 B、 C、 D、10. 一个不透明的盒子内装中有除颜色外,其余完全相同的个红球,个白球,个黄球,小星将盒中小球搅匀后,每次从中随机摸出一球,记下颜色后放回盒中搅匀,再从中随机摸出一球下面是他前两次摸球的情况:当小星第三次摸球时,下列说法正确的是( )
A、 B、 C、 D、8. 若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、9. 化简的结果是( )A、 B、 C、 D、10. 一个不透明的盒子内装中有除颜色外,其余完全相同的个红球,个白球,个黄球,小星将盒中小球搅匀后,每次从中随机摸出一球,记下颜色后放回盒中搅匀,再从中随机摸出一球下面是他前两次摸球的情况:当小星第三次摸球时,下列说法正确的是( )次数
第次
第次
第次
颜色
红球
红球
?
A、一定摸到红球 B、摸到红球的可能性小
C、一定摸不到红球 D、摸到红球、白球、黄球的可能性一样大11. 如图,以点为圆心,的长为半径画弧,与射线交于点 , 再以点为圆心,的长为半径画弧,两弧交于 , 两点,连接 , 则的长是( ) A、 B、 C、 D、12. 如图,网格中每个小正方形的边长均为 , , , , 四点均在格点上,与相交于点 , 则图中阴影部分的面积是( )
A、 B、 C、 D、12. 如图,网格中每个小正方形的边长均为 , , , , 四点均在格点上,与相交于点 , 则图中阴影部分的面积是( )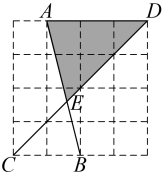 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共16.0分)
-
13. 不等式的解集为 .14. 如图,一次函数的图象经过第一、二、三象限,则的值可以是 写一个即可
 15. 毕业生小星、小华和小红准备拍照,他们三人随意站成一排,小华恰好站在中间的概率是 .16. 如图,在矩形纸片中,点 , 分别是边 , 上的点,连接 , 将四边形沿折叠,点的对应点恰好落在边上,点的对应点为点 , 连接若 , , 则的最小值是 .
15. 毕业生小星、小华和小红准备拍照,他们三人随意站成一排,小华恰好站在中间的概率是 .16. 如图,在矩形纸片中,点 , 分别是边 , 上的点,连接 , 将四边形沿折叠,点的对应点恰好落在边上,点的对应点为点 , 连接若 , , 则的最小值是 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算:;(2)、先化简,再求值: , 其中 .18. 如图,在正方形中,点 , 分别在 , 边上,且求证:≌ .
 19. 如图,在平面直角坐标系中,反比例函数的图象如图所示,矩形在第一象限内,平行于轴,且 , , 点的坐标为 .
19. 如图,在平面直角坐标系中,反比例函数的图象如图所示,矩形在第一象限内,平行于轴,且 , , 点的坐标为 . (1)、直接写出 , , 三点的坐标;
(1)、直接写出 , , 三点的坐标;
(2)、若将矩形向下平移个单位,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点?并求的值和反比例函数的表达式.20. 电信诈骗,严重危害着人民群众的财产安全,为提高大家的防范意识,某校举行了主题为“防电信诈骗,保财产安全”的知识测试七、八年级各有名学生,现从这两个年级各随机抽取名学生参加测试,为了解本次测试成绩的分布情况,将两个年级的测试成绩按: , : , : , :四个评价等级进行整理,得到了不完整的统计图表七年级成绩统计表:评价等级
成绩分
频数
频率
八年级测试成绩评价等级为的全部分数单位分如下: , , , , , , , , , , , , .
 (1)、表格中, ;
(1)、表格中, ;
(2)、八年级测试成绩的中位数是 ;
(3)、若测试成绩不低于分,则认为该学生对防电信诈骗意识较强,请估计该校七、八两个年级对防电信诈骗意识较强的学生一共有多少人?21. 爬山能强身健体,亲近自然,陶冶情操,王老师周末到公园爬山,山的形状如图 , 爬山路线示意图如图 , 王老师从山脚出发,沿走米到点,再沿到山顶点,已知山高为米, , , 交的延长线于点 , , 图中所有点均在同一平面内 (1)、求的长;
(1)、求的长;
(2)、求王老师从山脚点到达山顶点共走了多少米?结果精确到米参考数据: , ,22. 某校举行消防安全知识竞赛,竞赛试卷有选择和填空两种题型,共道,选择题每题分,填空题每题分,满分分.(1)、求选择题和填空题各有多少道?
(2)、竞赛规定,答对一道选择题得分,答对一道填空题得分,答错或不答一道题扣分,在这次竞赛中,小红填空题全部正确,被评为优秀分或分以上 , 小红至少答对了几道选择题?23. 如图,在中, , 以为直径的交于点 , 为的中点,连接 . (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、若 , , 求的半径;
(3)、在的条件下,求图中阴影部分的面积.24. 如图,在平面直角坐标系中,已知二次函数 , 顶点坐标为
(1)、若函数图象关于直线对称,求函数的表达式;
(2)、求的最大值;
(3)、是否存在实数 , 使得当时,二次函数的最大值为最小值的倍,若存在,求出;若不存在,请说明理由.25. 在菱形中, , 点为对角线的中点,为线段上的一个动点点不与点重合 , 分别过点 , 向直线作垂线和 , 垂足分别为点 , . (1)、【问题解决】:如图 , 当点在线段上,垂足与的中点重合,点与点重合时,求证:;
(1)、【问题解决】:如图 , 当点在线段上,垂足与的中点重合,点与点重合时,求证:;
(2)、【问题探究】:如图 , 当点在线段上,与还相等吗?如果相等,请证明如果不相等,请说明理由;
(3)、【拓展延伸】:当点在线段上运动, , 猜想线段 , , 之间有怎样的数量关系?并证明你的猜想.