贵州省黔东南州2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在 , , , 四个数中,负数有( )A、个 B、个 C、个 D、个2. 两地公路对汽车的行驶速度与明确的规定,规定最低时速不得低于公里,最高时速不得高于公里,用科学记数法可表示为( )A、 B、 C、 D、3. 如图是由个相同的正方体组成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算中正确的是( )A、 B、
4. 下列运算中正确的是( )A、 B、
C、 D、5. 如图,若 , 平分 , 则等于( )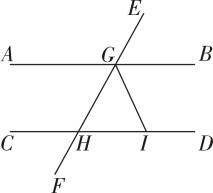 A、
A、
B、
C、
D、6. 炎热的夏天中午,在桌上放一杯开水,杯里的水温单位:与时间单位:的函数图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 某校某班开展一次演讲比赛,甲、乙、丙三名同学通过抽象决定出场顺序,则出场顺序恰好是甲乙丙的概率是( )A、 B、 C、 D、8. 如图,、、、是数轴上的点,那么在数轴上对应的点可能是( )
7. 某校某班开展一次演讲比赛,甲、乙、丙三名同学通过抽象决定出场顺序,则出场顺序恰好是甲乙丙的概率是( )A、 B、 C、 D、8. 如图,、、、是数轴上的点,那么在数轴上对应的点可能是( ) A、点 B、点 C、点 D、点9. 如图,在中, , , , 点是上的动点,则的最小值为( )
A、点 B、点 C、点 D、点9. 如图,在中, , , , 点是上的动点,则的最小值为( )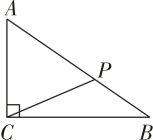 A、 B、 C、 D、10. 一个三角形的两边长分别为和 , 则第三边的长可能是( )A、 B、 C、 D、11. 如图,中,弦相交于点 , 则( ).
A、 B、 C、 D、10. 一个三角形的两边长分别为和 , 则第三边的长可能是( )A、 B、 C、 D、11. 如图,中,弦相交于点 , 则( ). A、 B、 C、 D、12. 在中,用尺规作图,分别以点和点为圆心,以大于的长为半径作弧,两弧相交于点和 , 作直线交于点 , 分别连接、、、、则下列结论不一定正确的是( )
A、 B、 C、 D、12. 在中,用尺规作图,分别以点和点为圆心,以大于的长为半径作弧,两弧相交于点和 , 作直线交于点 , 分别连接、、、、则下列结论不一定正确的是( ) A、 B、
A、 B、
C、 D、二、填空题(本大题共4小题,共16.0分)
-
13. 计算: .14. 若分式的值为0,则的值为 .15. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气体体积为2m3时,气压是 kPa.
 16. 如图,在菱形中,对角线 , 的长分别为 , , 将沿射线的方向平移得到 , 分别连接 , , , 则的最小值为 .
16. 如图,在菱形中,对角线 , 的长分别为 , , 将沿射线的方向平移得到 , 分别连接 , , , 则的最小值为 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算:;(2)、解不等式组: .18. 为了让学生了解文明礼仪知识,增强文明差异,养成文明习惯,某中学举行了一次“文明礼仪知识”竞赛,王老师为了解七年级本次竞赛的成绩情况,从中抽取部分学生的成绩,他将这部分学生的成绩分为个等级:待合格: , 合格: , 中: , 良: , 优: , 每个等级含左端点不含右端点,并绘制了如下两幅不完整的统计图:

请你根据上面的统计图解答下列问题:
(1)、扇形统计图中的 ;
(2)、补全频数分布直方图;
(3)、在符合格的名学生中有名女生和名男生,若从中抽取名同学调查不合格的原因,则抽到一名男生和一名女生的概率是多少?19. 如图,一次函数与反比例函数的图象交于 , 两点. (1)、求一次函数和反比例函数的解析式;
(1)、求一次函数和反比例函数的解析式;
(2)、根据图象直接写出的的取值范围.20. 年第届世界杯足球赛在卡塔尔举行,某商场在世界杯开始之前,用元购进 , 两种世界杯吉祥物共个,且用于购买种吉祥物与购买吉祥物的费用相同,且种吉祥物的单价是种吉祥物的倍.(1)、求 , 两种吉祥物的单价各是多少元?
(2)、世界杯开始后,商场的吉祥物很快就卖完了,于是计划用不超过元的资金再次购进 , 两种吉祥物共个,已知 , 两种吉祥物的进价不变求种吉祥物最多能购进多少个?21. 如图,将一张矩形纸片沿直线折叠,使点落在点处,点落在点处,直线交于点 , 交于点 . (1)、请写出图中一对全等的三角形;
(1)、请写出图中一对全等的三角形;
(2)、若 , , 求折痕的长.22. 如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道无人机从点的正上方点 , 沿正东方向以的速度飞行到达点 , 测得的俯角为 , 然后以同样的速度沿正东方向又飞行到达点 , 测得点的俯角为 .
 (1)、求无人机的高度结果保留根号;
(1)、求无人机的高度结果保留根号;
(2)、求的长度结果精确到 .
参考数据: , , ,23. 如图,内接于 , 交于点 , 交于点 , 交于点 , 连接 , .
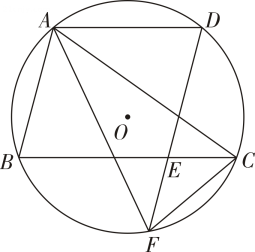 (1)、求证:;
(1)、求证:;
(2)、若的半径为 , , 求的长结果保留 .
