湖南省长沙市宁乡市2023年中考模拟数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在实数 , , , 中,为负数的是( )A、 B、 C、 D、2. 2022年3月11日,新华社发文总结2021年中国取得的科技成就,其中包括“奋斗者”号载人潜水器最深下潜至10909米.其中数据10909用科学记数法表示为( )A、10.909×102 B、1.0909×103 C、0.10909×104 D、1.0909×1043. 剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中,是中心对称图形的有( )
 A、 B、 C、 D、4. “青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想的青年学习行动某校为了解同学们某季度学习“青年大学习”的情况,从中随机抽取位同学,经统计他们的学习时间单位:分钟分别为: , , , , , , 则这组数据的众数为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶,古人认为,世间万物皆可分类归至八卦之中,相传,德国数学家莱布尼茨受八卦图的启发而发明了电子计算机使用的二进制.八卦图中的每一卦由三根线组成.如果从图中任选一卦,那么这一卦中恰有根“
A、 B、 C、 D、4. “青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想的青年学习行动某校为了解同学们某季度学习“青年大学习”的情况,从中随机抽取位同学,经统计他们的学习时间单位:分钟分别为: , , , , , , 则这组数据的众数为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶,古人认为,世间万物皆可分类归至八卦之中,相传,德国数学家莱布尼茨受八卦图的启发而发明了电子计算机使用的二进制.八卦图中的每一卦由三根线组成.如果从图中任选一卦,那么这一卦中恰有根“ ”和根“
”和根“ ”的概率是( )
”的概率是( ) A、 B、 C、 D、7. 把抛物线向左平移2个单位长度,平移后抛物线的表达式为( )A、 B、 C、 D、8. 如图,电线杆的中点处有一标志物,在地面处测得标志物的仰角为 , 若到电线杆底部的距离为米,则电线杆的长为( )
A、 B、 C、 D、7. 把抛物线向左平移2个单位长度,平移后抛物线的表达式为( )A、 B、 C、 D、8. 如图,电线杆的中点处有一标志物,在地面处测得标志物的仰角为 , 若到电线杆底部的距离为米,则电线杆的长为( ) A、米
A、米
B、米
C、米
D、米9. 若关于的一元一次不等式组有且只有个整数解,则符合条件的所有整数的和为( )A、 B、 C、 D、10. 如图,是的直径,点为圆上一点,是弧的中点,与交于点若是的中点,半径为 , 则的长为( ) A、
A、
B、
C、
D、二、填空题(本大题共6小题,共18.0分)
-
11. 要使代数式有意义,则的取值范围为 .12. 因式分解: .13. 若关于x的一元二次方程有一个根为0,则a的值等于 .14. 如图,用一个直径为的定滑轮拉动重物上升,滑轮旋转了 , 假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了 结果保留
 15. 若关于x的分式方程 =3的解是负数,则字母m的取值范围是.16. 如图,已知是内的一点, , , 若▱的面积为 , 且 , , 则的面积是 .
15. 若关于x的分式方程 =3的解是负数,则字母m的取值范围是.16. 如图,已知是内的一点, , , 若▱的面积为 , 且 , , 则的面积是 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
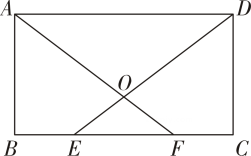
17. 计算: .18. 先化简,再求值: , 其中 .19. 如图:在矩形中, , 为上两点,且 , 连结 , 与交于点求证: .
 20. 如图矩形的顶点、分别在轴和轴上,点的坐标为 , 反比例函数的图象经过的中点 , 且与交于点 , .
20. 如图矩形的顶点、分别在轴和轴上,点的坐标为 , 反比例函数的图象经过的中点 , 且与交于点 , . (1)、求反比例函数的表达式及点的坐标.
(1)、求反比例函数的表达式及点的坐标.
(2)、若点是边上的一点,且为等腰三角形,求直线的表达式.21. 依据双减政策要求初中学生书面作业每天完成时间不超过分钟,某中学为了解学生作业管理情况随机调查了部分学生某天完成作业时长情况,根据调查结果,绘制成如下频数分布表和扇形统计图:请根据图表信息:解答下列问题:组别
每天作业完成时间分钟
人数
 (1)、表中 , , ;
(1)、表中 , , ;
(2)、扇形统计图中组所在扇形的圆心角是多少度?(3)、若该校有名学生,请估计书面作业平均完成时间低于分钟的学生人数.22. 为了推动长沙旅游业跨越发展,某旅行社推出“湖南博物院岳麓书院橘子洲”一日游活动团队旅游收费标准:如果人数不超过人,人均费用为元;如果超过人,每增加人,人均费用降低元,但人均费用不得低于元.(1)、当旅游人数为人时,人均费用为元,求的取值范围;
(2)、若某团队其支付旅游费用元,求该团队有多少人.23. 如图,是的直径,弦 , 垂足为点 , 直线与延长线交于点 , 且 . (1)、求证:直线是的切线;
(1)、求证:直线是的切线;
(2)、若 , , 求线段的长.24. 如图 , 正方形的边长为 , 为边上一动点点与点 , 不重合 , 连接交对角线于点 , 过点作交于点 , 连接 . (1)、求证:;
(1)、求证:;
(2)、如图 , 过点作于 , 在点的运动过程中,的长度是否发生变化?若不变,求出的长;若变化,请说明变化规律.
(3)、证明:在点的运动过程中,总有成立.25. 已知抛物线与轴交于点和 , 与轴交于点 .
 (1)、求抛物线的表达式;
(1)、求抛物线的表达式;
(2)、如图 , 点是线段上的一个动点不与点 , 重合 , 过点作轴的垂线交抛物线于点 , 联结 , 当四边形恰好是平行四边形时,求点的坐标;
(3)、如图 , 在的条件下,是的中点,过点的直线与抛物线交于点 , 且 , 在直线上是否存在点 , 使得与相似?若存在,求点的坐标;若不存在,请说明理由.