湖南省邵阳市隆回县2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列实数中小于的数是( )A、 B、 C、 D、2. 如图,直线 , 是截线,的度数是( )
 A、
A、
B、
C、
D、3. 下列图形中一定是轴对称图形的是( )A、梯形 B、直角三角形 C、等腰三角形 D、平行四边形4. 隆回县将大力实施“三高四新”战略,加快建设“三宜三融三区”现代化新隆回;到年,全县地区生产总值将突破亿元,亿用科学记数法可以表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、
C、 D、6. 在中,已知 , , 则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 一组数据8,3,8,6,7,8,7的众数和中位数分别是( )A、8,6 B、7,6 C、7,8 D、8,78. 若 , 则下列比例式中不正确的是( )A、 B、 C、 D、9. 下列说法正确的是( )A、相等的圆心角所对的弧相等 B、直径所对的圆周角是直角
C、内错角相等 D、相等的角是对顶角10. 若二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象为( )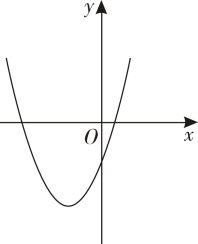 A、
A、 B、
B、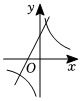 C、
C、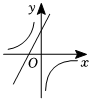 D、
D、
二、填空题(本大题共8小题,共24.0分)
-
11. 分解因式: .12. 式子 在实数范围内有意义,则 x 的取值范围是 .13. 一个多边形的内角和是它外角和的2倍,则它的边数是 .14. 已知菱形的两条对角线长分别为和 , 那么菱形的面积为 .15. 如图,在中,圆心角 , 那么圆周角 .
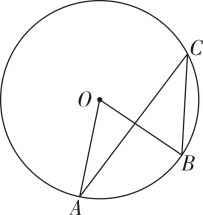 16. 如图,中,、分别在、上, , , , , 则 .
16. 如图,中,、分别在、上, , , , , 则 . 17. 已知 , 那么 .18. 观察下列数据: , , 它们是按一定规律排列的,依照此规律,第个数据是 .
17. 已知 , 那么 .18. 观察下列数据: , , 它们是按一定规律排列的,依照此规律,第个数据是 .三、解答题(本大题共8小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算: .20. 先化简 , 再在、、、中选择一个合适的的值代入求值.21. 如图,已知为的直径,为的切线,交于点 , 的延长线交于点 .
 (1)、求证:;
(1)、求证:;
(2)、若 , 求的长和的半径.22. 某地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵元,用元购买甲种物品的件数恰好与用元购买乙种物品的件数相同.(1)、求甲、乙两种救灾物品每件的价格各是多少元?
(2)、经调查,灾区对乙种物品件数的需求量是甲种物品件数的倍,若该爱心组织按照此需求的比例购买这件物品,需筹集资金多少元?23. 某校为了解九年级男生“坐位体前屈”项目的训练情况,随机抽取该年级部分男生进行了一次测试满分分,成绩均记为整数分 , 并按测试成绩单位:分分成四类:类 , 类 , 类 , 类绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题: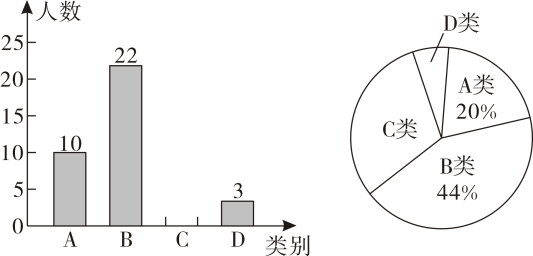 (1)、请求出本次一共抽取了多少学生,并补全条形统计图.
(1)、请求出本次一共抽取了多少学生,并补全条形统计图.
(2)、请求出类和类所占的百分比并求扇形统计图中类所对的圆心角的度数.
(3)、若该校九年级男生有名,估计该校九年级男生“坐位体前屈”项目成绩为类的有多少名?24. 如图,大海中某灯塔周围海里范围内有暗礁,一艘海轮在点处观察灯塔在北偏东方向,该海轮向正东方向航行海里到达点处,这时观察灯塔恰好在北偏东方向如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由参考数据:

