湖南省怀化市2023年中考三模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 对称美是和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,下列大学的校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 年国务院政府工作报告回顾了年取得的成就,工作回顾中提到“十四五”实现良好开局,人民生活水平稳步提高,脱贫攻坚成果得到巩固和拓展,新开工改造城镇老旧小区万个,惠及近千万家庭这个数万用科学记数法表示为数据来源百度百科年国务院政府工作报告 . ( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、
3. 年国务院政府工作报告回顾了年取得的成就,工作回顾中提到“十四五”实现良好开局,人民生活水平稳步提高,脱贫攻坚成果得到巩固和拓展,新开工改造城镇老旧小区万个,惠及近千万家庭这个数万用科学记数法表示为数据来源百度百科年国务院政府工作报告 . ( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、
C、 D、5. 以下调查中,最适合采用抽样调查的是( )A、了解全国中学生的视力和用眼卫生情况 B、了解全班50名同学每天体育锻炼的时间 C、学校招聘教师,对应聘人员进行面试 D、为保证飞机正常飞行,对其零部件进行检查6. 如图,直线 , , , 则的大小是( ) A、 B、 C、 D、7. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
A、 B、 C、 D、7. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )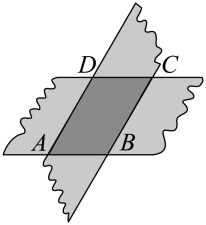 A、四边形周长不变 B、 C、四边形面积不变 D、8. 如图,、、是的切线,切点分别是、、若 , , 则的长是( )
A、四边形周长不变 B、 C、四边形面积不变 D、8. 如图,、、是的切线,切点分别是、、若 , , 则的长是( ) A、 B、 C、 D、9. “盈不足问题”作为我国数学的古典问题,在多年前的九章算术一书中就有很详尽而深刻的阐述书中记载:今有人买鸡,人出九,盈十一;人出六,不足十六问人数、物价各几何?意思是:有若干人一起买鸡,如果每人出文钱,就多出文钱;如果每人出文钱,就相差文钱买鸡的人数、鸡的价钱各是多少?若设鸡的价钱是文钱,根据题意列一元一次方程正确的是( )A、 B、 C、 D、10. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
A、 B、 C、 D、9. “盈不足问题”作为我国数学的古典问题,在多年前的九章算术一书中就有很详尽而深刻的阐述书中记载:今有人买鸡,人出九,盈十一;人出六,不足十六问人数、物价各几何?意思是:有若干人一起买鸡,如果每人出文钱,就多出文钱;如果每人出文钱,就相差文钱买鸡的人数、鸡的价钱各是多少?若设鸡的价钱是文钱,根据题意列一元一次方程正确的是( )A、 B、 C、 D、10. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
;
;
;
将图象向上平移个单位后与直线有个交点.A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 单项式 的系数是 .12. 分解因式: .13. 已知是二元一次方程的一个解,那么k的值是 .14. 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦 长20厘米,弓形高 为2厘米,则镜面半径为 厘米.
 15. 近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多为了解南迁到该区域某湿地的种候鸟的情况,从中捕捉只,戴上识别卡并放回;经过一段时间后观察发现,只种候鸟中有只佩有识别卡,由此估计该湿地约有 只种候鸟.16. 刘徽是我国魏晋时期伟大的数学家,他在九章算术注中指出:“勾、股幂合为弦幂,明矣”也就是说,图中直角三角形的三边、、存在的关系他在书中构造了一些基本图形来解决问题如图 , 分别将以为边长的正方形和为边长的正方形置于以为边长的大正方形的左下角和右上角,则图中阴影部分面积等于 用含字母的代数式表示;若 , 则 .
15. 近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多为了解南迁到该区域某湿地的种候鸟的情况,从中捕捉只,戴上识别卡并放回;经过一段时间后观察发现,只种候鸟中有只佩有识别卡,由此估计该湿地约有 只种候鸟.16. 刘徽是我国魏晋时期伟大的数学家,他在九章算术注中指出:“勾、股幂合为弦幂,明矣”也就是说,图中直角三角形的三边、、存在的关系他在书中构造了一些基本图形来解决问题如图 , 分别将以为边长的正方形和为边长的正方形置于以为边长的大正方形的左下角和右上角,则图中阴影部分面积等于 用含字母的代数式表示;若 , 则 .
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 先化简,再求值: , 其中 , .19. 如图所示,工人赵师傅用块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙、和、 , 点在上,已知 , .
 (1)、求证:≌;
(1)、求证:≌;
(2)、求的长.20. 我国的教育方针是:教育必须为社会主义现代化建设服务,为人民服务,与生产劳动和社会实践相结合,培养德智体美劳全面发展的社会主义建设者和接班人.为培养德智体美劳全面发展的优秀人才,丰都某中学开展了一系列精品课程,其中有一门课程《研学旅行》开展以来引起广泛关注,九年级2班数学兴趣小组对本班同学对《研学旅行》课的喜欢程度进行了调查,根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题: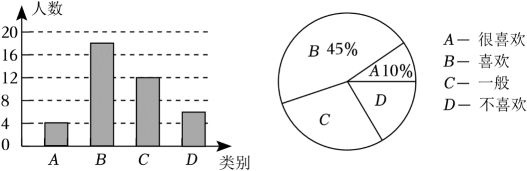 (1)、九年级2班共有学生名;(2)、九年级共有学生1200人,根据上述调查结果,估计九年级学生选择D类的大约有多少人?(3)、该校德育处决定从九年级二班调查的A类的4人中,抽2人到八年级开展研学宣讲,若在调查的A类4人中,刚好有2名男生2名女生,用画树状图或列表的方法求抽到的一男一女的概率.21. 如图,在中,点 , 分别是 , 的中点,点是延长线上的一点,且 , 连接 , .
(1)、九年级2班共有学生名;(2)、九年级共有学生1200人,根据上述调查结果,估计九年级学生选择D类的大约有多少人?(3)、该校德育处决定从九年级二班调查的A类的4人中,抽2人到八年级开展研学宣讲,若在调查的A类4人中,刚好有2名男生2名女生,用画树状图或列表的方法求抽到的一男一女的概率.21. 如图,在中,点 , 分别是 , 的中点,点是延长线上的一点,且 , 连接 , . (1)、求证:四边形是平行四边形;
(1)、求证:四边形是平行四边形;
(2)、若 , , , 求四边形的面积.22. 在平面直角坐标系中,直线:过 , , 直线: . (1)、求直线的表达式;
(1)、求直线的表达式;
(2)、过动点且垂直于轴的直线与 , 的交点分别是 , 当时,点位于点右方,直接写出的取值范围.23. 某班在庆祝中国共产主义青年团成立100周年活动中,给学生发放笔记本和钢笔作为纪念品.已知每本笔记本比每支钢笔多2元,用240元购买的笔记本数量与用200元购买的钢笔数量相同.(1)、笔记本和钢笔的单价各多少元?(2)、若给全班50名学生每人发放一本笔记本或一支钢笔作为本次活动的纪念品,要使购买纪念品的总费用不超过540元,最多可以购买多少本笔记本?24. 如图,内接于 , 的平分线交于点 , 交于点 , 且过点作 , 交的延长线于点 .
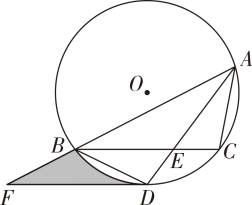 (1)、求证:为的切线;
(1)、求证:为的切线;
(2)、若 , , 求图中阴影部分的面积.25. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点 是函数 的图象的“等值点”.(1)、分别判断函数 的图象上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、设函数 的图象的“等值点”分别为点A,B,过点B作 轴,垂足为C.当 的面积为3时,求b的值;(3)、若函数 的图象记为 ,将其沿直线 翻折后的图象记为 .当 两部分组成的图象上恰有2个“等值点”时,直接写出m的取值范围.