湖南省张家界市桑植县2023年中考模拟数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 2023的绝对值为( )A、2023 B、 C、 D、2. 如图所示几何体,从左面看是( )
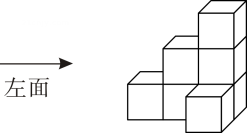 A、
A、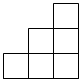 B、
B、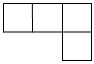 C、
C、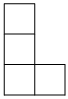 D、
D、 3. 2022年12月4日,神舟十四号载人飞船返回舱在东风着陆场成功着陆,本次载人飞行任务取得圆满成功,下列航天图标中,是中心对称图形的是( )A、
3. 2022年12月4日,神舟十四号载人飞船返回舱在东风着陆场成功着陆,本次载人飞行任务取得圆满成功,下列航天图标中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查中,适合采用全面调查的是( )A、调查陕西省各中小学垃圾分类的情况
4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查中,适合采用全面调查的是( )A、调查陕西省各中小学垃圾分类的情况
B、防疫期间对进入校园的人员进行体温检测
C、调查中央电视台开学第一课的收视率
D、调查咸阳湖的水质情况6. 已知不等式组 , 其解集在数轴上表示正确的是( )A、 B、
B、
C、 D、
D、 7. 如图,是的直径,垂直弦于点 , 的延长线交于点若 , , 则的长是( )
7. 如图,是的直径,垂直弦于点 , 的延长线交于点若 , , 则的长是( ) A、
A、
B、
C、
D、8. 已知二次函数与轴的一个交点为 , 其对称轴为直线 , 其部分图象如图所示,有下列个结论:
;
;
;
;
若有解、满足 , 则 , ;
其中正确的个数有( )A、个 B、个 C、个 D、个二、填空题(本大题共6小题,共18.0分)
-
9. 因式分解: =.10. 如图,一块飞镖游戏板由大小相等的小正方形格子构成向游戏板随机投掷一枚飞镖每次飞镖均落在纸板上 , 则击中阴影区域的概率是 .
 11. 新冠病毒的直径大约是米长,用科学记数法表示为 .12. 一副直角三角板如上图放置,点在的延长线上, , , , , 则
11. 新冠病毒的直径大约是米长,用科学记数法表示为 .12. 一副直角三角板如上图放置,点在的延长线上, , , , , 则 13. 如图,点是反比例函数图象上的一点,过点的直线与轴交于点 , 与反比例函数的图象交于点、 , 若 , 则的值为 .
13. 如图,点是反比例函数图象上的一点,过点的直线与轴交于点 , 与反比例函数的图象交于点、 , 若 , 则的值为 . 14. 如图,正方形的边长为 , 点 , 分别在 , 上, , 连接、 , 与相交于点 , 连接 , 取的中点 , 连接 , 则的长为 .
14. 如图,正方形的边长为 , 点 , 分别在 , 上, , 连接、 , 与相交于点 , 连接 , 取的中点 , 连接 , 则的长为 .
三、解答题(本大题共9小题,共58.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算16. 先化简,再求值: , 请在范围内选择一个你喜欢的整数代入求值.17. 年月日首届湖南旅游发展大会开幕式在张家界市隆重举行,“山娃娃”和“鲵宝宝”被选为此次活动的吉祥物某零售商店第一次用元购进一批山娃娃挂件若干个,第二次用购进鲵宝宝挂件是购进山娃娃挂件数量的 , 而鲵宝宝挂件的进货单价比山娃娃挂件的进货单价多元.(1)、求该商店购进的山娃娃和鲵宝宝数量各多少个?
(2)、该商店两种挂件的零售价都是元个,山娃娃挂件中有个因为损坏不能售出,其余都已售出,则鲵宝宝挂件要至少售出多少个,才能使这两次的总利润不低于元?18. 年月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“弦图”,该图被誉为“中国数学界的图腾”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如图为“弦图”的一部分,在正方形中, , . (1)、证明≌;
(1)、证明≌;
(2)、连接 , 若 , 求证: .19. 为了启发学生的阅读自觉性,培养学生的学习毅力,学校决定开展“读书月”活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成五类:艺术、文学、科普、传记、其他根据调查结果绘制了两幅不完整的统计图每位同学必选且只选最喜欢的一类 , 根据图中提供的信息,解答下列问题: (1)、这次调查的学生共有 名;
(1)、这次调查的学生共有 名;
(2)、补全条形统计图;
(3)、在扇形统计图中“科普”类所对应的圆心角的度数是 , “其他”类所对应的百分比是 ;
(4)、如果要从喜欢艺术的名同学中随机抽取名同学进行交流名男同学,名女同学 , 请用列表或树状图的方法,求所抽取的学生中恰有一名男生和一名女生的概率.20. 如图, 是 的直径,点 是劣弧 中点, 与 相交于点 .连接 与 的延长线相交于点 .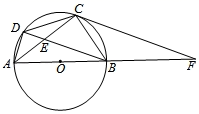 (1)、求证: 是 的切线;(2)、求证: ;(3)、若 ,求 的长.21. 如图,某地政府为解决当地农户网络销售农产品物流不畅问题,计划打通一条东西方向的隧道 , 无人机从点的正上方点 , 沿正东方向以的速度飞行到达点 , 测得的俯角为 , 然后以同样的速度沿正东方向又飞行到达点 , 测得点的俯角为 .
(1)、求证: 是 的切线;(2)、求证: ;(3)、若 ,求 的长.21. 如图,某地政府为解决当地农户网络销售农产品物流不畅问题,计划打通一条东西方向的隧道 , 无人机从点的正上方点 , 沿正东方向以的速度飞行到达点 , 测得的俯角为 , 然后以同样的速度沿正东方向又飞行到达点 , 测得点的俯角为 . (1)、求无人机的高度结果保留根号;
(1)、求无人机的高度结果保留根号;
(2)、求的长度结果精确到 , 参考数据: , , , .
