湖南省岳阳市三县六区2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 下列运算一定正确的是( )A、 B、
C、 D、3. 据世界卫生组织2020年6月26日通报,全球新冠肺炎确诊人数达到941万人,将数据941万人,用科学记数法表示为( )A、 人 B、 人 C、 人 D、 人4. 如图所示的几何体,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 从 , , , , 五个数中,随机抽取一个数,抽到无理数的概率是( )A、 B、 C、 D、6. 按一定规律排列的一列数依次是 、1、 、 、 、 …按此规律,这列数中第100个数是( )A、 B、 C、 D、7. 已知一次函数 , 二次函数若时,恒成立,则的取值范围是( )A、或 B、且
5. 从 , , , , 五个数中,随机抽取一个数,抽到无理数的概率是( )A、 B、 C、 D、6. 按一定规律排列的一列数依次是 、1、 、 、 、 …按此规律,这列数中第100个数是( )A、 B、 C、 D、7. 已知一次函数 , 二次函数若时,恒成立,则的取值范围是( )A、或 B、且
C、 D、二、填空题(本大题共8小题,共32.0分)
-
8. 函数中,自变量取值范围是 .9. 分解因式: .10. 为了中考“跳绳”项目能得到满分,小明练习了次跳绳,每次跳绳的个数如下单位:个: , , , , , 这次数据的中位数是 .11. 的解集是 .12. 请阅读下列材料,解答问题:
克罗狄斯托勒密约年年 , 是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理.
托勒密定理:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.
如图,正五边形内接于 , , 则对角线的长为 .
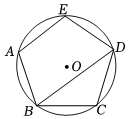 13. 如图,是的外接圆,平分交于点 , 交于点 , 的平分线交于点 , 过点作的切线 .
13. 如图,是的外接圆,平分交于点 , 交于点 , 的平分线交于点 , 过点作的切线 .
若的半径为 , , 则扇形的面积为 .
若 , , 则 .三、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
-
14. 计算15. 如图,在平行四边形中,点是边上一点不与 , 重合 , 过点作 , 交边于点 , 且 , .
 (1)、求证:四边形是矩形;
(1)、求证:四边形是矩形;
(2)、求证: .16. 已知一次函数与反比例函数相交于和两点,且点坐标为 , 点的横坐标为 .
 (1)、求反比例函数和一次函数的解析式;
(1)、求反比例函数和一次函数的解析式;
(2)、根据图象直接写出使得时,的取值范围.17. 国家规定“中小学生每天在校体育活动时间不低于小时”为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内一部分初中学生,分成四个小组表示时间,单位:小时组:;组:;组:;组:并将调查结果绘制成两幅不完整的统计图请你根据图中提供的信息,解答下列问题: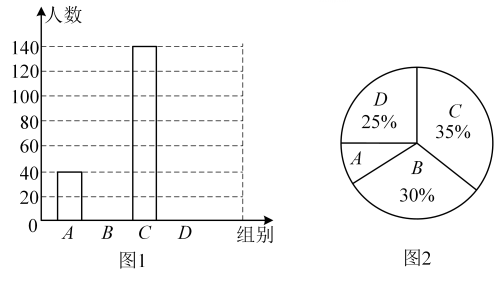 (1)、本次共抽取 名学生,其中组有 人,组有 人
(1)、本次共抽取 名学生,其中组有 人,组有 人
(2)、请你补全图统计图.
(3)、本次调查数据的中位数落在 组内.
(4)、若该市辖区内约有名初中学生,请你估计其中达到国家规定体育活动时间的学生约有多少人.18. 如图,某大楼的顶部有一块广告牌 , 小背在山坡的坡脚处测得广告牌底部的仰角为 , 沿坡面向上走到处测得广告牌顶部的仰角为已知山坡的坡度为 , 米,米.
 (1)、求点距地面的高度;
(1)、求点距地面的高度;
(2)、求广告牌的高度结果保留根号19. 有公共顶点的正方形与正方形按如图所示放置,点 , 分别在边和上,连接 , , 点是的中点,连接交于点 .
 (1)、线段与之间的数量关系是 ,位置关系是 ;(2)、将图中的正方形绕点顺时针旋转 , 线段与之间的数量关系和位置关系是否仍然成立?并说明理由.(3)、若正方形的边长为 , 将其沿翻折,点的对应点恰好落在边上,有最小值吗?有的话求出最小值,没有的话请说明理由.20. 如图,在平面直角坐标系中,抛物线与轴交于点、 , 与轴交于点是抛物线对称轴上一点,纵坐标为 , 是线段上方抛物线上的一个动点,连接、 .
(1)、线段与之间的数量关系是 ,位置关系是 ;(2)、将图中的正方形绕点顺时针旋转 , 线段与之间的数量关系和位置关系是否仍然成立?并说明理由.(3)、若正方形的边长为 , 将其沿翻折,点的对应点恰好落在边上,有最小值吗?有的话求出最小值,没有的话请说明理由.20. 如图,在平面直角坐标系中,抛物线与轴交于点、 , 与轴交于点是抛物线对称轴上一点,纵坐标为 , 是线段上方抛物线上的一个动点,连接、 . (1)、求抛物线的函数解析式;
(1)、求抛物线的函数解析式;
(2)、当与的面积相等时,求点的坐标;
(3)、将抛物线向左平移个单位,再向下平移个单位新抛物线与轴交于、两点点在点左侧 , 与轴交于点 , 是新抛物线上一动点,是坐标平面上一点,当以备用图点、、、为顶点的四边形是矩形时,请写出所有满足条件的点的坐标.