甘肃省庆阳市2023年中考一模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在实数 $- 3.5$ ， $- 2$ ， $0$ ， $2$ 中，最小的数是（）

A、 $- 3.5$ B、 $- 2$ C、 $0$ D、 $2$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \cdot a^{3} = 2 a^{3}$ C、 $a^{6} \div a^{3} = a^{3}$ D、 $(- 2 a^{2})^{3} = - 6 a^{6}$

查看试题解析
3. 在一些美术字中，有的汉字是轴对称图形．下面 $4$ 个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 1 \end{array}$ 的解，则 $a - b$ 的值是（）

A、 $- 1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
5. 下面命题正确的是（）

A、矩形对角线互相垂直
B、方程 $x^{2} = 14 x$ 的解为 $x = 14$ C、六边形内角和为 $540 °$ D、一对直角三角形，有一组斜边和直角边对应相等，则这两个直角三角形全等

查看试题解析
6. 如图，在 $△ A B C$ 中，点 $D$ 在边 $A B$ 上， $B D = 2 A D$ ， $D E / / B C$ 交 $A C$ 于点 $E$ ，若线段 $D E = 4$ ，则线段 $B C$ 的长为（）

A、 $7.5$ B、 $10$ C、 $12$ D、 $15$

查看试题解析
7. 把不等式组 ${\begin{cases} x + 1 \leq 3 \\ - 2 x - 6 < - 4 \end{cases}$ 中每个不等式的解集在同一条数轴上表示出来，正确的为（）

A、 B、 C、 D、

查看试题解析
8. 如图，在 $⊙ O$ 中， $A B$ 为弦， $O D ⊥ A B$ 于点 $D$ ， $∠ B O D = 53 °$ ，过点 $A$ 作 $⊙ O$ 的切线，交 $O D$ 的延长线于点 $C$ ，则 $∠ C =$ （）

A、 $27 °$ B、 $37 °$ C、 $43 °$ D、 $53 °$

查看试题解析
9. 如图，这是一农村民居侧面截图，屋坡 $A F$ ， $A G$ 分别架在墙体的点 $B$ ， $C$ 处，且 $A B = A C$ ，侧面四边形 $B D E C$ 为矩形 $.$ 若测得 $∠ F B D = 55 °$ ，则 $∠ A =$ （）

A、 $70 °$ B、 $110 °$ C、 $125 °$ D、 $135 °$

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为 $2 c m$ ，动点 $P$ ， $Q$ 同时从点 $A$ 出发，在正方形的边上，分别按 $A \to D \to C$ ， $A \to B \to C$ 的方向，都以 $1 c m / s$ 的速度运动，到达点 $C$ 运动终止，连接 $P Q$ ，设运动时间为 $x s$ ， $△ A P Q$ 的面积为 $y c m^{2}$ ，则下列图象中能大致表示 $y$ 与 $x$ 的函数关系的是（）

A、 B、 C、 D、

查看试题解析

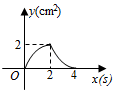
二、填空题（本大题共8小题，共24.0分）

11. 计算 $\sqrt{{(- 2)}^{2}}$ 的结果是.

查看试题解析
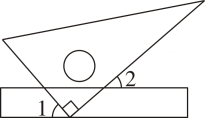
12. 分解因式： $b^{3} - b =$ .

查看试题解析
13. 如图，将一块三角板的直角顶点放在直尺的一边上，当 $∠ 2 = 40 °$ 时， $∠ 1 =$ $° .$

查看试题解析

14. 某公司

10

名职工的

3

月份工资统计如下，该公司

10

名职工

3

月份工资的中位数是元

.

工资 $/$ 元	$5000$	$5200$	$5400$	$5600$
人数 $/$ 人	$1$	$3$	$4$	$2$

查看试题解析

15. 关于 $x$ 的一元二次方程 $x^{2} + x + k = 0$ 有两个实数根，则 $k$ 的取值范围是．

查看试题解析
16. 已知点 $(- 2 ， y_{1})$ ， $(- 1 ， y_{2})$ ， $(1 ， y_{3})$ 都在反比例函数 $y = - \frac{m^{2}}{x} (m$ 为常数，且 $m \neq 0)$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是．

查看试题解析
17. 如图是某风景区的一个圆拱形门，路面AB宽为2m，净高CD为5m，则圆拱形门所在圆的半径为 m．

查看试题解析
18. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $B D = 8$ ， $t a n ∠ A B D = \frac{3}{4}$ ，则线段 $A B$ 的长为．

查看试题解析

三、计算题（本大题共1小题，共4.0分）

19. 解方程： $x (2 x - 5) = 2 x - 5$ ．

查看试题解析

四、解答题（本大题共9小题，共62.0分。解答应写出文字说明，证明过程或演算步骤）

20. 化简： $\frac{x^{2} - 4 x + 4}{x + 1} \div (1 - \frac{3}{x + 1})$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、尺规作图：在 $B C$ 边上求一点 $P$ ，使得 $P A = P C . ($ 保留作图痕迹，不写作法 $)$

(2)、求证： $△ A B C$ ∽ $△ P A C$ ．

查看试题解析
22. 如图，轮船沿正南方向以 $30$ 海里 $/$ 时的速度匀速航行，在 $M$ 处观测到灯塔 $P$ 在其南偏西 $22 °$ 方向上，航行 $2$ 小时后到达 $N$ 处，观测到灯塔 $P$ 在其南偏西 $44 °$ 方向上，若该船继续向南航行至离灯塔最近的位置，求此时轮船离灯塔的距离 $($ 由科学计算器得到 $s i n 68 ° \approx 0.9272$ ， $s i n 46 ° \approx 0.7193$ ， $s i n 44 ° \approx 0.6947$ ， $s i n 22 ° \approx 0.3746)$ ．

查看试题解析
23. 为落实国家“双减”政策，某学校在课后服务活动中开设了 $A$ 书法、 $B$ 剪纸、 $C$ 足球、 $D$ 乒乓球这四门课程供学生选择，每门课程被选到的机会均等．

(1)、小军选择的课程是篮球这一事件是▲ ；
$A$ .随机事件
$B$ .必然事件
$C$ .不可能事件

(2)、若小军和小贤两位同学各计划选修自己喜欢的一门课程，请用列表法或画树状图法求他们两人恰好同时选修球类课程的概率．

查看试题解析

24. 7为了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表：

组别	分组 $($ 单位：元 $)$	人数
$A$	$0 \leq x < 30$	$4$
$B$	$30 \leq x < 60$	$16$
$C$	$60 \leq x < 90$	$a$
$D$	$90 \leq x < 120$	$b$
$E$	$x \geq 120$	$2$

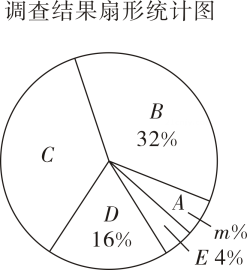
请根据以上图表，解答下列问题：

(1)、这次被调查的同学共有 ▲ 人，

a + b =

▲ ，

m % =

▲

%

；

(2)、求扇形统计图中扇形

C

的圆心角的度数；

(3)、若该校共有学生

1000

人，请估计每月零花钱的数额

x

在

30 \leq x < 90

范围的人数．

查看试题解析

25. 如图，一次函数的图象 $y = k x + b$ 与反比例函数 $y = \frac{a}{x}$ 的图象在第一象限交于点 $A (4 ， 3)$ ，与 $y$ 轴的负半轴交于点 $B$ ，且 $O A = O B$ ．

(1)、求一次函数 $y = k x + b$ 与反比例函数 $y = \frac{a}{x}$ 的表达式；

(2)、请直接写出不等式 $0 < k x + b < \frac{a}{x}$ 的解集．

查看试题解析
26. 如图，在 $△ A B C$ 中， $A B = A C .$ 以 $A B$ 为直径的 $⊙ O$ 分别与 $B C$ 、 $A C$ 相交于点 $D$ 、 $E$ ，连接 $A D .$ 过点 $D$ 作 $D F ⊥ A C$ ，垂足为点 $F$ ，

(1)、求证： $D F$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为 $4$ ， $∠ C D F = 22.5 °$ ，求图中阴影部分的面积．

查看试题解析
27. 如图，在▱ $A B C D$ 中， $∠ A C B = 45 °$ ， $A E ⊥ B C$ 于点 $E$ ，过点 $C$ 作 $C F ⊥ A B$ 于点 $F$ ，交 $A E$ 于点 $M$ ，点 $N$ 在边 $B C$ 上，且 $A M = C N$ ，连接 $D N$ ，延长 $A D$ 到点 $G$ ，使 $D G = N C$ ，连接 $C G$ ．

(1)、求证： $A B = C M$ ；

(2)、试判断 $△ A C G$ 的形状，并说明理由．

(3)、若 $A D = 3 \sqrt{2}$ ， $A M = \sqrt{2}$ ，则 $D N =$ ▲ ．

查看试题解析
28. 如图，过点 $A (5 ， \frac{15}{4})$ 的抛物线 $y = a x^{2} + b x$ 的对称轴是直线 $x = 2$ ，点 $B$ 是抛物线与 $x$ 轴的一个交点，点 $C$ 在 $y$ 轴上，点 $D$ 是抛物线的顶点，设点 $P$ 在直线 $O A$ 下方且在抛物线 $y = a x^{2} + b x$ 上，过点 $P$ 作 $y$ 轴的平行线交 $O A$ 于点 $Q$ ．

(1)、求 $a$ 、 $b$ 的值；

(2)、求 $P Q$ 的最大值；

(3)、当 $△ B C D$ 是直角三角形时，求 $△ O B C$ 的面积．

查看试题解析