【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练：第9题

试卷更新日期：2023-10-09 类型：二轮复习

进入出卷网下载

一、原题（多选题）

1. 已知圆锥的顶点为 $P$ ，底面圆心为 $O$ ， $A ， B$ 为底面直径， $∠ A P B = 120 °$ ， $P A = 2$ ，点 $C$ 在底面圆周上，且二面角 $P - A C - O$ 为45°，则（）

A、该圆锥的体积为 $π$ B、该圆锥的侧面积为 $4 \sqrt{3} π$ C、 $A C = 2 \sqrt{2}$ D、 $△ P A C$ 的面积为 $\sqrt{3}$

查看试题解析

二、基础

2. 已知圆锥顶点为S，底面圆心为 $O ， A C$ 为底面的直径， $A C = 6 ， S A$ 与底面所成的角为 $60 °$ ，则（）

A、 $S O = 3 \sqrt{3}$ B、该圆锥的母线长为6 C、该圆锥的体积为 $27 \sqrt{3} π$ D、该圆锥的侧面积为 $36 π$

查看试题解析
3. 已知圆锥的底面半径为2，其侧面展开图为一个半圆，则下列说法正确的是（）

A、圆锥的母线长是4 B、圆锥的高是 $\sqrt{2}$ C、圆锥的表面积是 $16 π$ D、圆锥的体积是 $\frac{8 \sqrt{3}}{3} π$

查看试题解析
4. 如图，已知圆锥SO母线长l＝5，底面半径r＝4，则下列结论中正确的有（）

A、圆锥的表面积为 $36 π$ B、圆锥侧面展开图的圆心角为 $\frac{8 π}{5}$ C、圆锥的体积为 $16 π$ D、圆锥的轴截面是锐角三角形

查看试题解析
5. 已知圆台的上底半径为1，下底半径为3，球O与圆台的两个底面和侧面都相切，则（）

A、圆台的母线长为4 B、圆台的高为4 C、圆台的表面积为 $26 π$ D、球O的体积为 $12 π$

查看试题解析
6. 陀螺是中国民间最早的娱乐工具之一，也作陀罗，闽南语称作“干乐”，北方叫作“冰尜（gá）”或“打老牛”．传统古陀螺大致是木制或铁制的倒圆锥形．现有一圆锥形陀螺（如图所示），其底面半径为3，将其放倒在一平面上，使圆锥在此平面内绕圆锥顶点S滚动，当圆锥在平面内转回原位置时，圆锥本身恰好滚动了3周，则（）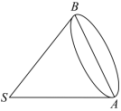

A、圆锥的母线长为 9 B、圆锥的表面积为 $36 π$ C、圆锥的侧面展开图（扇形）的圆心角为60° D、圆锥的体积为 $12 \sqrt{2} π$

查看试题解析
7. 如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等，下列结论正确的是（）

A、圆柱的侧面积为 $2 π R^{2}$ B、圆锥的侧面积为 $2 π R^{2}$ C、圆柱的侧面积与球面面积相等 D、圆柱、圆锥、球的体积之比为3：1：2

查看试题解析
8. 已知三棱锥 $P - ABC$ 的体积为1，其外接球 $O$ 的半径为 $R$ ， $PA = 2R$ ， $Δ ABC$ 是腰长为2的等腰三角形，且 $∠ BAC = \frac{2π}{3}$ ，则

A、球 $O$ 的体积为 $\frac{2 \sqrt{19}}{3} π$ B、球 $O$ 的表面积为 $\frac{19}{2} π$ C、球 $O$ 的表面积为19π D、球 $O$ 的体积为 $\frac{19 \sqrt{19}}{6} π$

查看试题解析
9. 如图，在圆锥SO中，AC为底面圆O的直径，B是圆O上异于A，C的一点， $O C = 3$ ， $S O = 3 \sqrt{3}$ ，则下列结论中一定正确的是（）

A、圆锥 $S O$ 的体积为 $9 \sqrt{3} π$ B、圆锥 $S O$ 的表面积为 $18 π$ C、三棱锥 $S - A B C$ 的体积的最大值为 $9 \sqrt{3}$ D、存在点B使得直线SB与平面SAC所成角为 $\frac{π}{4}$

查看试题解析
10. 在《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马，如图，四棱锥 $P - A B C D$ 为一个阳马，其中 $P A ⊥$ 平面 $A B C D$ ， $A E ⊥ P B$ ， $A F ⊥ P C$ ， $A M ⊥ P D$ ， $E ， F ， M$ 均为垂足，则（）

A、四棱锥 $P - A B C D$ 的外接球直径为 $P C$ B、三棱锥 $P - E F M$ 的外接球体积大于三棱锥 $A - E F M$ 的外接球体积 C、 $A ， B ， C ， D ， E ， F ， M$ 七点在同一个球面上 D、平面 $E F M ∥$ 平面 $A B C D$

查看试题解析
11. 如图所示，外层是类似于“甜筒冰激凌”的图形，上部分是体积为 $10 \sqrt{15} π$ 的半球，下面大圆刚好与高度为6的圆锥的底面圆重合，在该封闭的几何体内倒放一个小圆锥，小圆锥底面平行于外层圆锥的底面，且小圆锥顶点与外层圆锥顶点重合，则该小圆锥体积可以为（）

A、10π B、18π C、30π D、40π

查看试题解析
12. 已知点 $P$ ， $C$ ， $D$ 是圆锥表面上的点，该圆锥的侧而展开图为以点 $P$ 为圆心， $4$ 为半径的半圆，点 $C$ 是 $\overset{⌢}{A B}$ 的中点，点 $D$ 是 $\overset{⌢}{A C}$ 的中点（如图），则下列说法正确的是（）

A、圆锥的体积为 $\frac{8 \sqrt{3}}{3} π$ B、直线 $P D$ 与圆锥底面夹角为 $\frac{π}{6}$ C、圆锥的内切球半径为 $\frac{2 \sqrt{3}}{3}$ D、以圆锥底面圆心为球心､半径为2的球被平面 $P C D$ 所截，则截面面积为 $\frac{16}{7} π$

查看试题解析
13. 如图所示， $A B$ 是圆锥 $S O$ 底面圆 $O$ 的一条直径，点 $C$ 在底面圆周上运动（异于 $A 、 B$ 两点），以下说法正确的是（）

A、 $∠ C S O$ 恒为定值 B、三棱锥 $S - A B C$ 的体积存在最大值 C、圆锥 $S O$ 的侧面积大于底面圆 $O$ 的面积 D、 $△ S A B$ 的面积大于 $△ S A C$ 的面积

查看试题解析
14. 某圆锥的底面半径为4，母线长为5，则下列关于此圆锥的说法正确的是（）

A、圆锥的体积为 $16 π$ B、圆锥的侧面展开图的圆心角为 $\frac{4 π}{5}$ C、圆锥的侧面积为 $10 π$ D、过圆锥两条母线的截面面积最大值为 $\frac{25}{2}$

查看试题解析
15. 如图， $A C$ 为圆锥 $S O$ 的底面圆O的直径，点B是圆O上异于A，C的动点， $S O = O C = 2$ ，则下列结论正确的是（）

A、圆锥 $S O$ 的侧面积为 $4 \sqrt{2} π$ B、三棱锥 $S - A B C$ 体积的最大值为8 C、 $∠ S A B$ 的取值范围是 $(\frac{π}{4} ， \frac{π}{3})$ D、若 $A B = B C$ ，E为线段 $A B$ 上的动点，则 $S E + C E$ 的最小值为 $2 (\sqrt{3} + 1)$

查看试题解析

三、提升

16. 已知正四面体 $P - A B C$ 的棱长为2，下列说法正确的是（）

A、正四面体 $P - A B C$ 的外接球表面积为 $6 π$ B、正四面体 $P - A B C$ 内任意一点到四个面的距离之和为定值 C、正四面体 $P - A B C$ 的相邻两个面所成二面角的正弦值为 $\frac{1}{3}$ D、正四面体 $Q - M N G$ 在正四面体 $P - A B C$ 的内部，且可以任意转动，则正四面体 $Q - M N G$ 的体积最大值为 $\frac{2 \sqrt{2}}{81}$

查看试题解析
17. 《几何原本》是古希腊数学家欧几里得的数学著作，其中第十一卷称轴截面为等腰直角三角形的圆锥为直角圆锥.如图， $A B$ ， $C D$ 是直角圆锥 $S O$ 底面圆的两条不同的直径，下列说法正确的是（）

A、存在某条直径 $C D$ ，使得 $A D ⊥ S D$ B、若 $A B = 2$ ，则三棱锥 $S - A O D$ 体积的最大值为 $\frac{1}{6}$ C、对于任意直径 $C D$ ，直线 $A D$ 与直线 $S B$ 互为异面直线 D、若 $∠ A B D = \frac{π}{6}$ ，则异面直线 $S A$ 与 $C D$ 所成角的余弦值是 $\frac{\sqrt{2}}{4}$

查看试题解析
18. 已知圆台的上下底面的圆周都在半径为2的球面上，圆台的下底面过球心，上底面半径为 $r (0 < r < 2)$ ，设圆台的体积为V，则下列选项中说法正确的是（）

A、当 $r = 1$ 时， $V = 7 \sqrt{3} π$ B、V存在最大值 C、当r在区间 $(0 ， 2)$ 内变化时，V逐渐减小 D、当r在区间 $(0 ， 2)$ 内变化时，V先增大后减小

查看试题解析
19. 已知 $A B$ 为圆锥 $S O$ 底面圆 $O$ 的直径，点 $C$ 是圆 $O$ 上异于 $A$ ， $B$ 的一点， $N$ 为 $S A$ 的中点， $S A = 5$ ，圆锥 $S O$ 的侧面积为 $15 π$ ，则下列说法正确的是（）

A、圆 $O$ 上存在点 $M$ 使 $M N / /$ 平面 $S B C$ B、圆 $O$ 上存在点 $M$ 使 $A M ⊥$ 平面 $S B C$ C、圆锥 $S O$ 的外接球表面积为 $\frac{625 π}{32}$ D、棱长为 $\sqrt{6}$ 的正四面体在圆锥 $S O$ 内可以任意转动

查看试题解析
20. 折扇在我国已有三四千年的历史，“扇”与“善”谐音，折扇也寓意“善良”“善行”．它以字画的形式集中体现了我国文化的方方面面，是运筹帷幄，决胜千里，大智大勇的象征（如图1）．图2是一个圆台的侧面展开图（扇形的一部分），若扇形的两个圆弧所在圆的半径分别是1和3，且 $∠ A B C = 120 °$ ，则该圆台（）

A、高为 $\frac{2 \sqrt{2}}{3}$ B、表面积为 $\frac{34 π}{9}$ C、体积为 $\frac{52 \sqrt{2}}{81} π$ D、上底面积、下底面积和侧面积之比为 $1 ： 9 ： 24$

查看试题解析
21. 在三棱柱 $ABC - A_{1} B_{1} C_{1}$ 中，底面 $ABC$ 为正三角形，侧棱垂直于底面， $E$ 是 $AB$ 的中点， $O$ 是 $B C_{1}$ 的中点．给出下列结论正确的是（）

A、若 $P$ 是 $A C_{1}$ 上的动点，则 $OP$ 与 $A_{1} B_{1}$ 异面 B、 $A C_{1} //$ 平面 $B_{1} CE$ C、若该三棱柱有内切球，则 $AB ： A A_{1} = 1 ： \sqrt{3}$ D、若该三棱柱所有棱长均相等，则侧面对角线与棱成 $45 °$ 角的共有30对

查看试题解析
22. 已知圆台的轴截面如图所示，其上、下底面半径分别为 $r_{上} = 1$ ， $r_{下} = 2$ ，母线 $A B$ 长为2，点 $E$ 为 $A B$ 的中点，则（）

A、圆台的体积为 $\frac{7 \sqrt{3}}{3} π$ B、圆台的侧面积为 $12 π$ C、圆台母线 $A B$ 与底面所成角为60° D、在圆台的侧面上，从点 $C$ 到点 $E$ 的最短路径长为4

查看试题解析
23. 在三棱锥 $A - B C D$ 中， $A B = C D = \sqrt{2}$ ， $A D = B C = A C = B D = \sqrt{5}$ ，则（）

A、 $A B ⊥ C D$ B、三棱锥 $A - B C D$ 的体积为 $\frac{2}{3}$ C、三棱锥 $A - B C D$ 外接球半径为 $\sqrt{6}$ D、异面直线 $A D$ 与 $B C$ 所成角的余弦值为 $\frac{3}{5}$

查看试题解析
24. 若正方体ABCD-A₁B₁C₁D₁的棱长为1，则下列命题正确的是（）

A、直线BC与平面ABC₁D₁所成的角为 $\frac{π}{4}$ B、点C到平面ABC₁D₁的距离为 $\frac{\sqrt{2}}{2}$ C、异面直线D₁C和BC₁所成的角为 $\frac{π}{4}$ D、三棱柱AA₁D₁- BB₁C₁外接球半径为 $\frac{\sqrt{3}}{2}$

查看试题解析
25. 用与母线不垂直的两个平行平面截一个圆柱，若两个截面都是椭圆形状，则称夹在这两个平行平面之间的几何体为斜圆柱．这两个截面称为斜圆柱的底面，两底面之间的距离称为斜圆柱的高，斜圆柱的体积等于底面积乘以高．椭圆的面积等于长半轴与短半轴长之积的 $π$ 倍，已知某圆柱的底面半径为2，用与母线成45°角的两个平行平面去截该圆柱，得到一个高为6的斜圆柱，对于这个斜圆柱，下列选项正确的是（）

A、底面椭圆的离心率为 $\frac{\sqrt{2}}{2}$ B、侧面积为 $24 \sqrt{2} π$ C、在该斜圆柱内半径最大的球的表面积为 $36 π$ D、底面积为 $4 \sqrt{2} π$

查看试题解析

四、培优

26. 某班级到一工厂参加社会实践劳动，加工出如图所示的圆台 $O_{1} O_{2}$ ，在轴截面ABCD中， $A B = A D = B C = 2 c m$ ，且 $C D = 2 A B$ ，下列说法正确的是（）

A、该圆台轴截 $A B C D$ 面面积为 $3 \sqrt{3} c m^{2}$ B、该圆台的体积为 $\frac{7 \sqrt{3} π}{3} c m^{3}$ C、该圆台的表面积为 $10 π c m^{2}$ D、沿着该圆台表面，从点 $C$ 到 $A D$ 中点的最短距离为 $5 c m$

查看试题解析
27. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $4 ， O$ 为空间中任一点，则下列结论中正确的是（）

A、若 $O$ 为线段 $A C$ 上任一点，则 $A_{1} O$ 与 $B C$ 所成角的余弦值范围为 $[0 ， \frac{\sqrt{3}}{3}]$ B、若 $O$ 为正方形 $A D D_{1} A_{1}$ 的中心，则三棱锥 $O - A B D$ 外接球的体积为 $\frac{64 \sqrt{2}}{3} π$ C、若 $O$ 在正方形 $D C C_{1} D_{1}$ 内部，且 $| O B | = 2 \sqrt{6}$ ，则点 $O$ 轨迹的长度为 $\sqrt{2} π$ D、若三棱锥 $O - B D C_{1}$ 的体积为 $\frac{32}{3} ， ∠ O D_{1} C = \frac{π}{6}$ 恒成立，点 $O$ 轨迹的为圆的一部分

查看试题解析
28. 勒洛Franz Reuleaux（1829～1905），德国机械工程专家，机构运动学的创始人.他所著的《理论运动学》对机械元件的运动过程进行了系统的分析，成为机械工程方面的名著.勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触，因此它能像球一样来回滚动.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体.如图所示，设正四面体 $A B C D$ 的棱长为2，则下列说法正确的是（）

A、勒洛四面体能够容纳的最大球的半径为 $2 - \frac{\sqrt{6}}{2}$ B、勒洛四面体被平面 $A B C$ 截得的截面面积是 $2 (π - \sqrt{3})$ C、勒洛四面体表面上交线 $A C$ 的长度为 $\frac{2 π}{3}$ D、勒洛四面体表面上任意两点间的距离可能大于2

查看试题解析
29. 如图，在五面体 $P Q A B C D$ 中，底面 $A B C D$ 为矩形， $△ A D P$ 和 $△ B C Q$ 均为等边三角形， $P Q / /$ 平面 $A B C D$ ， $A B = 7$ ， $A D = 2 \sqrt{3}$ ，且二面角 $P - A D - C$ 和 $Q - B C - A$ 的大小均为 $θ (θ ∈ (0 ， π))$ ．设五面体 $P Q A B C D$ 的各个顶点均位于球 $O$ 的表面上，则（）

A、有且仅有一个 $θ$ ，使得五面体 $P Q A B C D$ 为三棱柱 B、有且仅有两个 $θ$ ，使得平面 $A D P ⊥$ 平面 $B C Q$ C、当 $c o s θ = - \frac{1}{4}$ 时，五面体 $P Q A B C D$ 的体积取得最大值 D、当 $c o s θ = 0$ 时，球 $O$ 的半径取得最小值

查看试题解析
30. 如图，两个底面为矩形的四棱锥 $S - A B C D$ 、 $S_{1} - A B C D$ 组合成一个新的多面体 $Γ$ ，其中 $△ S A D$ 、 $△ S_{1} B C$ 为等边三角形，其余各面为全等的等腰直角三角形.平面 $α / /$ 平面 $S A D$ ，平面 $α$ 截多面体 $Γ$ 所得截面多边形的周长为 $L$ ，则下列结论正确的有（）

A、 $S B ⊥ B C$ B、 $S C ⊥ A B$ C、多面体 $Γ$ 有外接球 D、 $L$ 为定值

查看试题解析
31. 如图所示，在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，P，Q分别为棱AB，BC的中点，则以下四个结论正确的是（）

A、棱 $C_{1} D_{1}$ 上存在一点M，使得 $A M$ //平面 $B_{1} P Q$ B、直线 $A_{1} C_{1}$ 到平面 $B_{1} P Q$ 的距离为 $\frac{2}{3}$ C、过 $A_{1} C_{1}$ 且与面 $B_{1} P Q$ 平行的平面截正方体所得截面面积为 $\frac{9}{8}$ D、过PQ的平面截正方体的外接球所得截面面积的最小值为 $\frac{3 π}{8}$

查看试题解析
32. 如图，AC为圆锥SO底面圆O的直径，点B是圆O上异于A，C的动点， $S O = O C = 2$ ，则下列结论正确的是（）

A、圆锥SO的侧面积为 $4 \sqrt{2} π$ B、三棱锥 $S - A B C$ 体积的最大值为 $\frac{8}{3}$ C、 $∠ S A B$ 的取值范围是 $(\frac{π}{4} ， \frac{π}{3})$ D、若 $A B = B C$ ， E为线段AB上的动点，则 $S E + C E$ 的最小值为 $2 (\sqrt{3} + 1)$

查看试题解析