吉林省吉林市2023-2024学年八年级上学期第一次月考数学试卷
试卷更新日期:2023-10-09 类型:月考试卷
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图,在中, , , 则的度数为( )
 A、 B、 C、 D、2. 如图,中, , 为上一点,于点 , 下列说法中,错误的是( )
A、 B、 C、 D、2. 如图,中, , 为上一点,于点 , 下列说法中,错误的是( ) A、中,是上的高 B、中,是上的高 C、中,是上的高 D、中,是上的高3. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )
A、中,是上的高 B、中,是上的高 C、中,是上的高 D、中,是上的高3. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )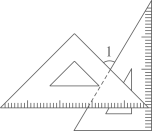 A、 B、 C、 D、4. 如图,点E、点F在上, , , 添加一个条件,不能证明的是( )
A、 B、 C、 D、4. 如图,点E、点F在上, , , 添加一个条件,不能证明的是( ) A、 B、 C、 D、5. 如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A、 B、 C、 D、5. 如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )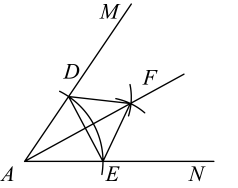 A、 B、 C、 D、6. 图中表示被撕掉一块的正边形纸片,若 , 则的值是( )
A、 B、 C、 D、6. 图中表示被撕掉一块的正边形纸片,若 , 则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
7. 如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
 8. 一个三角形的两边长分别是和 , 则第三边长可以是 写出一个即可9. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.
8. 一个三角形的两边长分别是和 , 则第三边长可以是 写出一个即可9. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.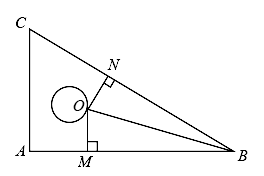 10. 如图,已知 , 点B,E,C,F依次在同一条直线上. 若 , , 则CF的长为.
10. 如图,已知 , 点B,E,C,F依次在同一条直线上. 若 , , 则CF的长为.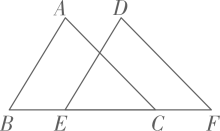 11. 将正六边形与正方形按如图所示摆放,且正六边形的边与正方形的边在同一条直线上,则的度数是 .
11. 将正六边形与正方形按如图所示摆放,且正六边形的边与正方形的边在同一条直线上,则的度数是 . 12. 如图,已知为的中线, , , 的周长为 , 则的周长为 .
12. 如图,已知为的中线, , , 的周长为 , 则的周长为 . 13. 如图,在中, , 平分交边于点 , 的面积为 , , 则线段的长度为 .
13. 如图,在中, , 平分交边于点 , 的面积为 , , 则线段的长度为 . 14. 如图所示, .
14. 如图所示, .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 已知一个多边形的内角和比外角和的倍多 , 则这个多边形的边数是多少?16. 如果一个三角形的一边长为 , 另一边长为 , 若第三边长为 .(1)、求第三边的范围;(2)、当第三边长为奇数时,求三角形的周长.17. 如图,在中, , , 是的角平分线,求的度数.
 18. 如图, , , , 求证 .
18. 如图, , , , 求证 . 19. 图为的网格,每一小格均为正方形,已知 .
19. 图为的网格,每一小格均为正方形,已知 .
⑴画出中边上的中线;
⑵画出中边上的高;
⑶直接写出的面积为 ▲ .
20. 如图,是内的一条射线,是上一点,过点作于点 , 于点 , 已知 , 求证:是的平分线. 21. 数学兴趣小组想在不用涉水的情况下测量某段河流的宽度该段河流两岸是平行的 , 在数学老师带领下他们是这样做的:
21. 数学兴趣小组想在不用涉水的情况下测量某段河流的宽度该段河流两岸是平行的 , 在数学老师带领下他们是这样做的:在河流的一条岸边点,选对岸正对的一棵树为参照点;
沿河岸直走有一棵树 , 继续前行到达处;
从处沿河岸垂直的方向行走,当到达树正好被树遮挡住的处停止行走;
测得的长为 .
 (1)、河流的宽度为;(2)、请你说明他们做法的正确性.22. 如图,在中, , 过点作 , 垂足为 , 延长至点使在边上截取 , 连接求证: .
(1)、河流的宽度为;(2)、请你说明他们做法的正确性.22. 如图,在中, , 过点作 , 垂足为 , 延长至点使在边上截取 , 连接求证: .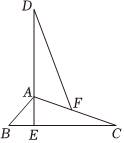 23. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .
23. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .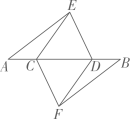 (1)、求证:;(2)、若 , , 求的长.24. 如图,已知 , , , 与交于点 .
(1)、求证:;(2)、若 , , 求的长.24. 如图,已知 , , , 与交于点 . (1)、求证:≌;(2)、若 , 求的度数.25. 如图,中,的角平分线与外角的平分线交于 .
(1)、求证:≌;(2)、若 , 求的度数.25. 如图,中,的角平分线与外角的平分线交于 .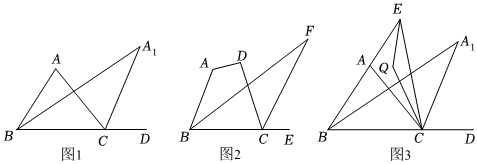 (1)、如图 , 若 , 则 .(2)、如图 , 四边形中,的角平分线及外角的角平分线相交于点 , 若 , 求的度数.(3)、如图 , 中,的角平分线与外角的角平分线交于 , 若为延长线上一动点,连接 , 与的角平分线交于点 , 当滑动时有下面两个结论:
(1)、如图 , 若 , 则 .(2)、如图 , 四边形中,的角平分线及外角的角平分线相交于点 , 若 , 求的度数.(3)、如图 , 中,的角平分线与外角的角平分线交于 , 若为延长线上一动点,连接 , 与的角平分线交于点 , 当滑动时有下面两个结论:的值为定值;
的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
26. 如图 (1)、模型的发现:
(1)、模型的发现:如图 , 在中, , , 直线经过点 , 且、两点在直线的同侧,直线 , 直线 , 垂足分别为点 , 请直接写出、和的数量关系.
(2)、模型的迁移:位置的改变如图 , 在的条件下,若 , 两点在直线的异侧,请说明、和的关系,并证明.
(3)、模型的迁移:角度的改变如图 , 在的条件下,若三个直角都变为了相等的钝角,即 , 其中 , 的结论还成立吗?若成立,请你给出证明;若不成立,请说明、和的关系,并证明.