云南省昆明市西山区2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
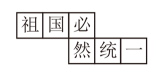
1. 下列四个选项中,为无理数的是( )A、 B、 C、 D、2. 习总书记说:“祖国一定统一,也必须统一”,这是亿中华儿女的共同心愿,也是中华民族伟大复兴的必然要求.我们把“祖国必然统一”六个字分别写在一个正方体的每个面上,如图是这个正方体的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
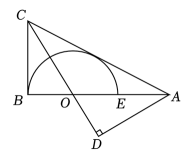
 A、祖 B、必 C、然 D、统3. 如图,在中,点 , 分别是 , 的中点,且 , , 则的度数为( )
A、祖 B、必 C、然 D、统3. 如图,在中,点 , 分别是 , 的中点,且 , , 则的度数为( )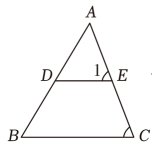 A、 B、 C、 D、4. 不等式组的解集在数轴上表示为( )A、
A、 B、 C、 D、4. 不等式组的解集在数轴上表示为( )A、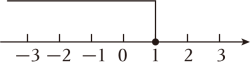 B、
B、 C、
C、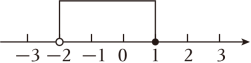 D、
D、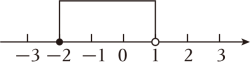 5. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、6. 如图,是直径, , 则为( )
5. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、6. 如图,是直径, , 则为( )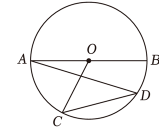 A、 B、 C、 D、7. 定义一种新运算: , 如 , 则的结果为( )A、 B、 C、 D、8. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,是格点三角形,则的值为( )
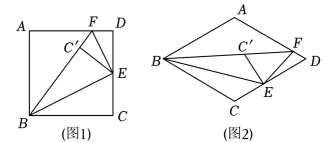
A、 B、 C、 D、7. 定义一种新运算: , 如 , 则的结果为( )A、 B、 C、 D、8. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,是格点三角形,则的值为( )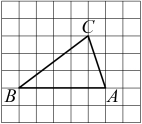 A、 B、 C、 D、9. 如图,已知零件的外径是 , 现用一个交叉卡钳两条尺长和相等测量零件的内孔直径如果::: , 且量得 , 则零件的厚度为 . ( )
A、 B、 C、 D、9. 如图,已知零件的外径是 , 现用一个交叉卡钳两条尺长和相等测量零件的内孔直径如果::: , 且量得 , 则零件的厚度为 . ( )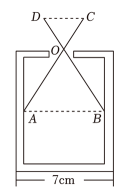 A、 B、 C、 D、10. 某公路发生山体滑坡,有米的路段被山石泥土掩盖,阻碍了正常的交通通行.甲乙两工程队接到的任务是:两工程队分别从两头开始各自抢修道路米.已知甲工程队每小时比乙工程队每小时多抢修米,且甲工程队比乙工程队早小时完成任务.求甲乙两工程队每小时分别抢修道路多少米?设甲工程队每小时抢修道路米,则列方程正确的是( )A、 B、 C、 D、11. 如图,在同一平面直角坐标系中,直线与双曲线相交于点和点 , 则当时,的取值范围是( )
A、 B、 C、 D、10. 某公路发生山体滑坡,有米的路段被山石泥土掩盖,阻碍了正常的交通通行.甲乙两工程队接到的任务是:两工程队分别从两头开始各自抢修道路米.已知甲工程队每小时比乙工程队每小时多抢修米,且甲工程队比乙工程队早小时完成任务.求甲乙两工程队每小时分别抢修道路多少米?设甲工程队每小时抢修道路米,则列方程正确的是( )A、 B、 C、 D、11. 如图,在同一平面直角坐标系中,直线与双曲线相交于点和点 , 则当时,的取值范围是( )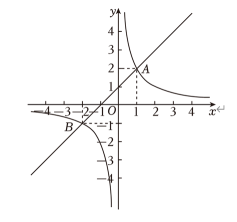 A、或 B、 C、或 D、或12. 如果矩形满足 , 那么矩形叫做“黄金矩形”如图,已知矩形是黄金矩形,对角线 , 相交于且 , 则关于黄金矩形 , 下列结论不正确的是( )
A、或 B、 C、或 D、或12. 如果矩形满足 , 那么矩形叫做“黄金矩形”如图,已知矩形是黄金矩形,对角线 , 相交于且 , 则关于黄金矩形 , 下列结论不正确的是( )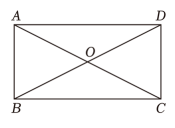 A、 B、 C、 D、矩形的周长
A、 B、 C、 D、矩形的周长二、填空题(本大题共4小题,共12.0分)
-
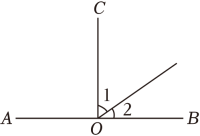
13. 如图,已知 , , 则 .
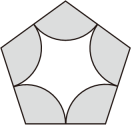
 14. 计算: .15. 下列调查中:①了解一批灯泡的使用寿命;②检测“神舟十五号”载人飞船的零件质量;③调查长江的水质情况;④调查某班学生的视力情况.应使用全面调查的是 .16. 如图,已知正五边形的边长为 , 则阴影部分的面积为 .
14. 计算: .15. 下列调查中:①了解一批灯泡的使用寿命;②检测“神舟十五号”载人飞船的零件质量;③调查长江的水质情况;④调查某班学生的视力情况.应使用全面调查的是 .16. 如图,已知正五边形的边长为 , 则阴影部分的面积为 .
三、计算题(本大题共1小题,共6.0分)
-
17. 计算: .
四、解答题(本大题共7小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
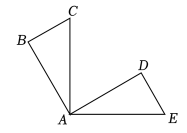
18. 如图,已知 , , , , 求证: .
 19. 置换反应是一种单质与一种化合物反应,生成另一种单质和另一种化合物的反应,包括金属与盐的反应,金属与酸的反应等,某化学实验课上,董老师带来了 , , , 四种金属.这四种金属分别用四个相同的不透明的容器装着,让同学们随机选择一种金属与盐酸反应来制取氢气.根据金属活动顺序可知: , 可以置换出氢气,而 , 则不能置换出氢气(1)、琪琪从四种金属中随机选择一种,则选到的概率为;(2)、琪琪和涵涵分别从四种金属中随机选择一种金属分别进行实验,请用列表法或树状图法求二人所选金属均能置换出氢气的概率.20. 月日是世界第个读书日,教育部发布了全国中小学生阅读指导目录.为了响应号召,学校开展了“书香进校园,校园读书月”活动,收到了良好的效果.学校学生会随机抽取若干同学进行了“学生平均每天阅读时间情况”的调查,并将调查结果绘作成尚不完整的图表如下:
19. 置换反应是一种单质与一种化合物反应,生成另一种单质和另一种化合物的反应,包括金属与盐的反应,金属与酸的反应等,某化学实验课上,董老师带来了 , , , 四种金属.这四种金属分别用四个相同的不透明的容器装着,让同学们随机选择一种金属与盐酸反应来制取氢气.根据金属活动顺序可知: , 可以置换出氢气,而 , 则不能置换出氢气(1)、琪琪从四种金属中随机选择一种,则选到的概率为;(2)、琪琪和涵涵分别从四种金属中随机选择一种金属分别进行实验,请用列表法或树状图法求二人所选金属均能置换出氢气的概率.20. 月日是世界第个读书日,教育部发布了全国中小学生阅读指导目录.为了响应号召,学校开展了“书香进校园,校园读书月”活动,收到了良好的效果.学校学生会随机抽取若干同学进行了“学生平均每天阅读时间情况”的调查,并将调查结果绘作成尚不完整的图表如下:类别
类别学生平均每天的阅读时间
频数
频率
合计
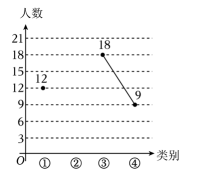
根据图表信息,完成下列问题.
(1)、 , , ;(2)、学生平均每天的阅读时间的中位数落在____填类别 , 并补全折线统计图;(3)、按照上面调查结果,试估计在开展“书香进校园,校园读书月”活动期间,该校名学生中平均每天阅读时间在小时包括小时以上的学生人数?21. 某杂技团进行杂技表演,演员从跷跷板的右端处弹跳起经过最高点后下落到右端的椅子处,其身体看成一点运动的路线是一条抛物线的一部分,如图,已知,演员起跳点的高度 , 演员离开地面的最大高度是 , 此时,演员到起跳点的水平距离为 . (1)、求该抛物线的解析式;(2)、已知人梯高 , 为了成功完成此次表演,那么人梯到起跳点的水平距离应为多少?
(1)、求该抛物线的解析式;(2)、已知人梯高 , 为了成功完成此次表演,那么人梯到起跳点的水平距离应为多少?
-