云南省临沧市临清市2023年中考三模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
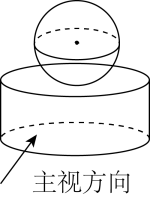
1. 下列各数是负数的是( )A、 B、 C、 D、2. 某几何体如图所示,它的俯视图是( )
 A、
A、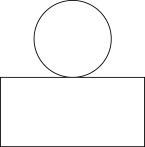 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,一块含有角的直角三角板放置在两条平行线上,若 , 则为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,一块含有角的直角三角板放置在两条平行线上,若 , 则为( )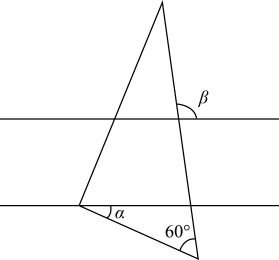 A、 B、 C、 D、5. 对于二次函数 , 当为和时,对应的函数值分别为和若 , 则与的大小关系是( )A、 B、 C、 D、无法比较6. 为了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类球的喜爱情况,小鹏采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息没有绘制完成,已知喜欢网球的人数少于喜欢足球的人数,根据如图所示的信息,这批被抽样调查的学生中喜欢足球的人数可能是( )
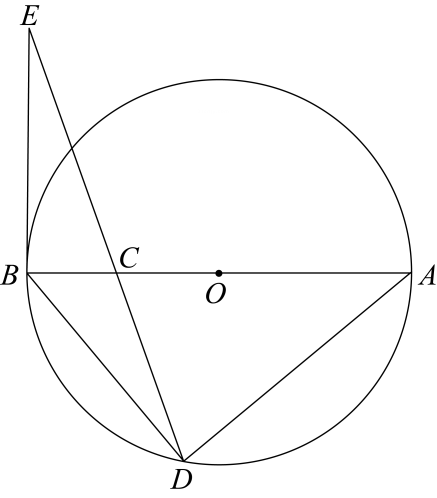
A、 B、 C、 D、5. 对于二次函数 , 当为和时,对应的函数值分别为和若 , 则与的大小关系是( )A、 B、 C、 D、无法比较6. 为了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类球的喜爱情况,小鹏采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息没有绘制完成,已知喜欢网球的人数少于喜欢足球的人数,根据如图所示的信息,这批被抽样调查的学生中喜欢足球的人数可能是( )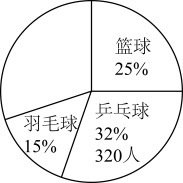 A、人 B、人 C、人 D、人7. 若是二元一次方程组的解,则为( )A、 B、 C、 D、8. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )
A、人 B、人 C、人 D、人7. 若是二元一次方程组的解,则为( )A、 B、 C、 D、8. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )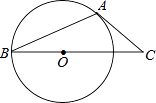 A、20° B、25° C、40° D、50°9. 已知a、b、c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是( )A、没有实数根 B、可能有且只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根10. 如图,点E在正方形 的边 上,将 绕点A顺时针旋转 到 的位置,连接 ,过点A作 的垂线,垂足为点H,与 交于点G.若 , ,则 的长为( )
A、20° B、25° C、40° D、50°9. 已知a、b、c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是( )A、没有实数根 B、可能有且只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根10. 如图,点E在正方形 的边 上,将 绕点A顺时针旋转 到 的位置,连接 ,过点A作 的垂线,垂足为点H,与 交于点G.若 , ,则 的长为( )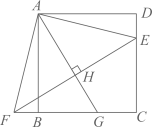 A、 B、 C、4 D、11. 在年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案边长为的正六边形放在平面直角坐标系中,若与轴垂直,顶点的坐标为 , 则顶点的坐标为( )
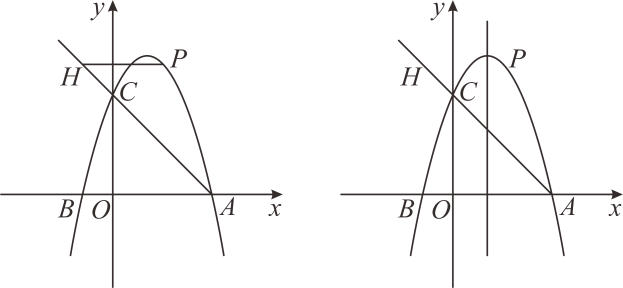
A、 B、 C、4 D、11. 在年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案边长为的正六边形放在平面直角坐标系中,若与轴垂直,顶点的坐标为 , 则顶点的坐标为( )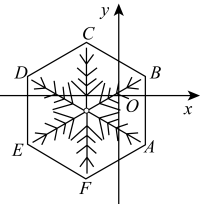 A、 B、 C、 D、12. 如图所示,为矩形的边上一点,动点 , 同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是秒,设 , 同时出发秒时,的面积为 , 已知与的函数关系图象如图曲线为抛物线的一部分 , 则下列结论不正确的是( )
A、 B、 C、 D、12. 如图所示,为矩形的边上一点,动点 , 同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是秒,设 , 同时出发秒时,的面积为 , 已知与的函数关系图象如图曲线为抛物线的一部分 , 则下列结论不正确的是( ) A、:: B、当秒时, C、当时, D、当的面积为时,的值是或秒
A、:: B、当秒时, C、当时, D、当的面积为时,的值是或秒二、填空题(本大题共5小题,共15.0分)
-
13. 不等式组的解集为.14. 从 , , 这个数中,任取两个数作为点的坐标,则点在第四象限的概率是 .15. 一元二次方程的两个根为 , , 则的值是 .16. 在中 , 以所在直线为轴,把旋转一周,得到圆锥,则该圆锥的侧面积为 .17. 如图,已知直线l:y= x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 .
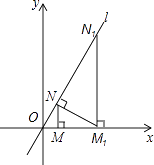
三、解答题(本大题共8小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 先化简后求值: , 其中 .19. 为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
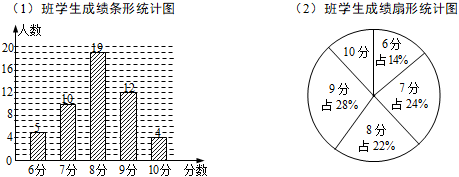 (1)、求(2)班学生中测试成绩为10分的人数;(2)、请确定下表中a,b,c的值(只要求写出求a的计算过程);
(1)、求(2)班学生中测试成绩为10分的人数;(2)、请确定下表中a,b,c的值(只要求写出求a的计算过程);统计量
平均数
众数
中位数
方差
(1)班
8
8
c
1.16
(2)班
a
b
8
1.56
(3)、从上表中选择合适的统计量,说明哪个班的成绩更均匀.20. 如图,菱形的对角线、相交于点 , 过点作 , 且 , 连接 . (1)、求证:四边形为矩形;
(1)、求证:四边形为矩形;
(2)、连接 , 若 , , 求的长.21. 习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知1件甲种农机具比1件乙种农机具多1.5万元,用18万元购买甲种农机具的数量和用12万元购买乙种农机具的数量相同.(1)、求购买1件甲种农机具和1件乙种农机具各需多少万元?(2)、若该粮食生产基地计划购买甲、乙两种农机具共20件,且购买的总费用不超过72.6万元,则甲种农机具最多能购买多少件?22. 某校数学社团开展“探索生活中的数学”研学活动,准备测量一栋大楼的高度.如图所示,其中观景平台斜坡的长是米,坡角为 , 斜坡底部与大楼底端的距离为米,与地面垂直的路灯的高度是米,从楼顶测得路灯顶端处的俯角是试求大楼的高度.
参考数据: , , , , ,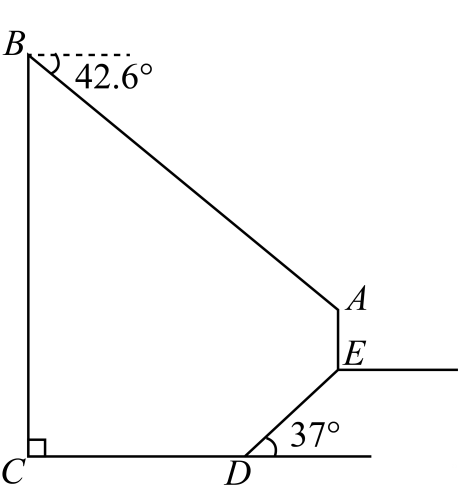 23. 如图,直线与反比例函数的图象交于 , 两点,过点作轴于点 , 过点作轴于点 .
23. 如图,直线与反比例函数的图象交于 , 两点,过点作轴于点 , 过点作轴于点 .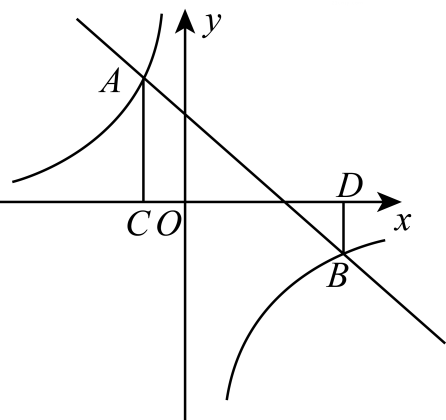 (1)、求 , 的值及反比例函数的解析式;
(1)、求 , 的值及反比例函数的解析式;
(2)、若点在直线上,且 , 请求出此时点的坐标.