云南省昭通市巧家县2023年中考数学二模考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,每小题3分,共36分)
-
1. 若二次根式有意义,则应满足的条件是( )A、 B、 C、 D、2. 如图, , 平分 , 为上一点,且 , 则的度数为( )
 A、 B、 C、 D、3. 据国家邮政局消息,2023年春运期间,全网累计揽收邮件快件103.67亿件,较2022年同期增长6.14%.将103.67亿用科学记数法可以表示为( )A、 B、 C、 D、4. 下列立体图形中,主视图不是中心对称图形的是( )A、
A、 B、 C、 D、3. 据国家邮政局消息,2023年春运期间,全网累计揽收邮件快件103.67亿件,较2022年同期增长6.14%.将103.67亿用科学记数法可以表示为( )A、 B、 C、 D、4. 下列立体图形中,主视图不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
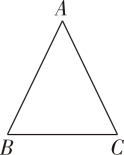
D、 5. 若一个多边形的外角和是它内角和的 , 则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在等腰中, , , , 则的值为( )
5. 若一个多边形的外角和是它内角和的 , 则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在等腰中, , , , 则的值为( )
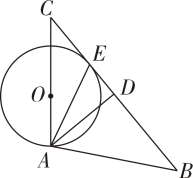
 A、 B、 C、 D、8. 下列说法错误的是( )A、若 , 则 B、要了解全省中小学学生的视力情况,应该采用抽样调查的方式 C、一组数据7,3,3,6,4的中位数和众数都是3 D、甲、乙两组跳高运动员身高数据的方差分别为 , , 则乙组队员的身高比较整齐9. 关于的一元二次方程的一个根为0,则的值为( )A、 B、 C、3 D、010. 观察下列代数式: , , , , …,根据其中的规律可得第2023个式子是( )A、 B、 C、 D、11. 如图,是以为底边的等腰三角形,点为的外心,连接交于点.若 , 则的长为( )
A、 B、 C、 D、8. 下列说法错误的是( )A、若 , 则 B、要了解全省中小学学生的视力情况,应该采用抽样调查的方式 C、一组数据7,3,3,6,4的中位数和众数都是3 D、甲、乙两组跳高运动员身高数据的方差分别为 , , 则乙组队员的身高比较整齐9. 关于的一元二次方程的一个根为0,则的值为( )A、 B、 C、3 D、010. 观察下列代数式: , , , , …,根据其中的规律可得第2023个式子是( )A、 B、 C、 D、11. 如图,是以为底边的等腰三角形,点为的外心,连接交于点.若 , 则的长为( ) A、 B、 C、3 D、212. 若关于的一元一次方程有整数解,且关于的不等式组有且只有三个整数解,则满足所有条件的整数的和是( )A、 B、6 C、12 D、
A、 B、 C、3 D、212. 若关于的一元一次方程有整数解,且关于的不等式组有且只有三个整数解,则满足所有条件的整数的和是( )A、 B、6 C、12 D、二、填空题(本大题共4小题,每小题2分,共8分)
-
13. 点关于轴的对称点为点 , 则点的坐标为.14. 因式分解m3n-mn3=.15. 如图,是的外接圆,为的直径,连接 , 若 , , 则的长为cm.
 16. 把一个母线长8cm,底面直径为10cm的圆锥模型展开后得到的扇形圆心角为.
16. 把一个母线长8cm,底面直径为10cm的圆锥模型展开后得到的扇形圆心角为.三、解答题(本大题共8小题,共56分)
-
17. 计算:.18. 如图,在四边形中,平分 , 点在线段上, , .求证:.
 19. 教育部办公厅提出《关于做好中小学生课后服务工作的指导意见》中指出,课后服务主要为安排学生做作业、自主阅读、体育、艺术、科普、拓展训练、开展社团及兴趣小组活动等.某校安排每周四的课后服务都是球类运动,为了解该校七年级学生对球类运动项目的喜爱程度,调查小组随机调查了该年级部分学生,根据调查结果绘制了如下扇形统计图和条形统计图:
19. 教育部办公厅提出《关于做好中小学生课后服务工作的指导意见》中指出,课后服务主要为安排学生做作业、自主阅读、体育、艺术、科普、拓展训练、开展社团及兴趣小组活动等.某校安排每周四的课后服务都是球类运动,为了解该校七年级学生对球类运动项目的喜爱程度,调查小组随机调查了该年级部分学生,根据调查结果绘制了如下扇形统计图和条形统计图:
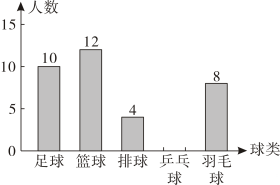 (1)、本次随机调查的学生共有人.(2)、补全条形统计图(标明数字).(3)、若该校七年级共有240人,求喜欢篮球的同学大约有多少人.20. 在一次复习《四边形》的习题课中,王老师准备了四张形状大小完全相同的卡片,正面分别写有A.平行四边形、B.矩形、C.菱形、D.正方形.现将这四张卡片背面朝上,洗匀后放在讲桌上,每位同学只能抽取一张,抽到哪一张就要背诵出该张卡片上所写四边形的性质.(1)、甲同学抽到写有“C.菱形”卡片的概率为.(2)、若王老师要求甲、乙两位同学同时抽取卡片并分别进行背诵,用画树状图法或列表法求甲、乙两人抽到的卡片中有写有“A.平行四边形”卡片的概率.21. 如图,菱形的对角线与交于点 , 于点 , 交于点 , 于点.
(1)、本次随机调查的学生共有人.(2)、补全条形统计图(标明数字).(3)、若该校七年级共有240人,求喜欢篮球的同学大约有多少人.20. 在一次复习《四边形》的习题课中,王老师准备了四张形状大小完全相同的卡片,正面分别写有A.平行四边形、B.矩形、C.菱形、D.正方形.现将这四张卡片背面朝上,洗匀后放在讲桌上,每位同学只能抽取一张,抽到哪一张就要背诵出该张卡片上所写四边形的性质.(1)、甲同学抽到写有“C.菱形”卡片的概率为.(2)、若王老师要求甲、乙两位同学同时抽取卡片并分别进行背诵,用画树状图法或列表法求甲、乙两人抽到的卡片中有写有“A.平行四边形”卡片的概率.21. 如图,菱形的对角线与交于点 , 于点 , 交于点 , 于点.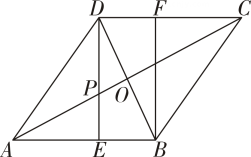 (1)、判断四边形的形状,并写出证明过程.(2)、若 , , 求的长,22. 随着电视剧《去有风的地方》的热播,大理旅游业持续升温.当地某度假村有简约型客房10间,后现代型客房30间.按现有标价,若两种客房全部都住满,则一天营业额为7500元;若两种客房均有10间入住,则一天营业额为3500元.(1)、简约型客房和后现代型客房标价分别为多少元?(2)、该度假村以后现代型客房为主营,根据调查发现,如果按原有标价,那么30间后现代型客房都会住满,当每间后现代型客房的标价增加10元时,就会空出一个房间,若度假村需对每间后现代型客房每天支出60元的各种费用,求每间后现代型客房标价为多少元时,后现代型客房每天的利润达到最大.
(1)、判断四边形的形状,并写出证明过程.(2)、若 , , 求的长,22. 随着电视剧《去有风的地方》的热播,大理旅游业持续升温.当地某度假村有简约型客房10间,后现代型客房30间.按现有标价,若两种客房全部都住满,则一天营业额为7500元;若两种客房均有10间入住,则一天营业额为3500元.(1)、简约型客房和后现代型客房标价分别为多少元?(2)、该度假村以后现代型客房为主营,根据调查发现,如果按原有标价,那么30间后现代型客房都会住满,当每间后现代型客房的标价增加10元时,就会空出一个房间,若度假村需对每间后现代型客房每天支出60元的各种费用,求每间后现代型客房标价为多少元时,后现代型客房每天的利润达到最大.