上海市嘉定区2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共6小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列关于的函数中,一定是二次函数的是( )A、 B、 C、 D、2. 抛物线一定经过点( )A、 B、 C、 D、 .3. 如果把三边的长度都扩大为原来的倍,那么锐角的四个三角比的值( )A、都扩大为原来的倍 B、都缩小为原来的
C、都没有变化 D、都不能确定4. 在中, , , , 那么的正弦值是( )A、 B、 C、 D、5. 已知非零向量、、 , 下列条件中不能判定的是( )A、 B、
C、 , D、 ,6. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共12小题,共48.0分)
-
7. 已知 , 那么 .8. 已知抛物线开口向下,那么的取值范围是 .9. 将抛物线向右平移个单位,得到的新抛物线表达式是 .10. 已知点、在二次函数的图象上,那么 填“”、“”、“” .11. 抛物线的对称轴是直线 , 如果此抛物线与轴的一个交点的坐标是 , 那么抛物线与轴的另一个交点的坐标是 .12. 已知在中, , , , 那么的长是 .13. 如图,在梯形中, , , , 如果 , , 那么 .
 14. 如图,某飞机在离地面垂直距离米的上空处,测得地面控制点的俯角为 , 那么飞机与该地面控制点之间的距离等于 米结果保留根号 .
14. 如图,某飞机在离地面垂直距离米的上空处,测得地面控制点的俯角为 , 那么飞机与该地面控制点之间的距离等于 米结果保留根号 . 15. 如图,已知在平行四边形中,点在边上,且 , 设 , , 那么 .
15. 如图,已知在平行四边形中,点在边上,且 , 设 , , 那么 .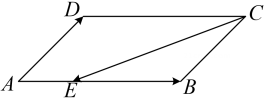 16. 如图,已知在中,、分别是、边上的中线,且相交于点 , 过点作 , 那么 .
16. 如图,已知在中,、分别是、边上的中线,且相交于点 , 过点作 , 那么 . 17. 如图,在中, , , 如果 , , 那么 .
17. 如图,在中, , , 如果 , , 那么 .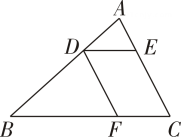 18. 在中, , , , 是边上的中线如图将绕着点逆时针旋转,使点落在线段上的点处,点落在点处,边与边交于点 , 那么的长是 .
18. 在中, , , , 是边上的中线如图将绕着点逆时针旋转,使点落在线段上的点处,点落在点处,边与边交于点 , 那么的长是 .
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算: .20. 已知二次函数的图象经过、、三点.
(1)、求这个函数的解析式;
(2)、用配方法求出这个二次函数图象的顶点坐标.21. 如图,已知在平行四边形中,是边上的一点,与相交于点 , 与的延长线相交于点 , , 求、的长. 22. 海岛算经是中国古代测量术的代表作,原名重差这本著作建立起了从直接测量向间接测量的桥梁直至近代,重差测量法仍有借鉴意义.
22. 海岛算经是中国古代测量术的代表作,原名重差这本著作建立起了从直接测量向间接测量的桥梁直至近代,重差测量法仍有借鉴意义.
如图 , 为测量海岛上一座山峰的高度,直立两根高米的标杆和 , 两杆间距相距米,、、三点共线从点处退行到点 , 观察山顶 , 发现、、三点共线,且仰角为;从点处退行到点 , 观察山顶 , 发现、、三点共线,且仰角为点、都在直线上 (1)、求的长结果保留根号;
(1)、求的长结果保留根号;
(2)、山峰高度的长结果精确到米参考数据: ,23. 如图,已知在中, , 点、分别在边、的延长线上,且 , 的延长线交于点 . (1)、求证:∽;
(1)、求证:∽;
(2)、如果 , 求证: .