上海市青浦区2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共6小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
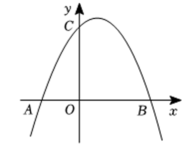
1. 已知三个数、、 , 如果再添上一个数,使它们能组成一个比例式,那么这个数可以是( )A、 B、 C、 D、2. 三角形的重心是( )A、三角形三条角平分线的交点 B、三角形三条中线的交点
C、三角形三条边的垂直平分线的交点 D、三角形三条高的交点3. 如果把一个锐角的三边的长都扩大为原来的倍,那么锐角的正弦值( )A、扩大为原来的倍 B、缩小为原来的 C、没有变化 D、不能确定4. 已知非零向量 , , , 下列条件中,不能判定向量与向量平行的是( )A、 , B、
C、 , D、5. 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )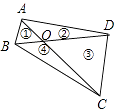 A、①与②相似 B、①与③相似 C、①与④相似 D、②与④相似6. 已知二次函数为常数 .
A、①与②相似 B、①与③相似 C、①与④相似 D、②与④相似6. 已知二次函数为常数 .
命题:该函数的图象经过点;命题:该函数的图象经过点;命题:该函数的图象与轴的交点位于轴的下方;命题:该函数的图象的对称轴为直线如果这四个命题中只有一个命题是假命题,那么这个假命题是( )A、命题 B、命题 C、命题 D、命题二、填空题(本大题共12小题,共48.0分)
-
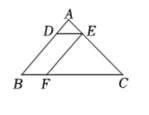
7. 如果:: , 那么: .8. 已知向量与单位向量方向相反,且 , 那么用向量的式子表示 .9. 如果两个相似三角形的周长比为1:2,那么它们的对应中线的比为.10. 如果抛物线经过原点,那么的值等于 .11. 抛物线在轴右侧的部分是 填“上升”或“下降”12. 将抛物线y=x2向左平移1个单位后的抛物线表达式为 .13. 在中, , 如果 , , 那么 .14. 如图,在中,点、、分别在边、、上, , , 如果 , 那么 .
 15. 如图,河堤横断面迎水坡的坡度是: , , 则坡面的长度是
15. 如图,河堤横断面迎水坡的坡度是: , , 则坡面的长度是 16. 如图,在矩形中, , 点、分别在边、上,点、在对角线上.如果四边形是菱形,那么线段的长为 .
16. 如图,在矩形中, , 点、分别在边、上,点、在对角线上.如果四边形是菱形,那么线段的长为 . 17. 如图,点是正方形内一点, , , 如果将线段绕点顺时针旋转 , 点的对应点为 , 射线交边于点 , 那么线段的长为 .
17. 如图,点是正方形内一点, , , 如果将线段绕点顺时针旋转 , 点的对应点为 , 射线交边于点 , 那么线段的长为 .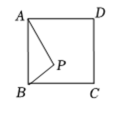 18. 定义:如图 , 点 , 把线段分割成、和 , 如果以、、为边的三角形是一个直角三角形,那么称点、是线段的勾股分割点问题:如图 , 在中,已知点、是边的勾股分割点线段 , 射线、与射线分别交于点、如果 , , , 那么:的值为 .
18. 定义:如图 , 点 , 把线段分割成、和 , 如果以、、为边的三角形是一个直角三角形,那么称点、是线段的勾股分割点问题:如图 , 在中,已知点、是边的勾股分割点线段 , 射线、与射线分别交于点、如果 , , , 那么:的值为 .
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算: .20. 如图,在平行四边形中,点在边上,射线、相交于点 , .
 (1)、求:的值;
(1)、求:的值;
(2)、如果 , , 试用、表示向量 .21. 如图,在中, , 垂足为点 , 平分交于点 , , , .
 (1)、求的值;
(1)、求的值;
(2)、求线段的长.22. 某校九年级数学兴趣小组在实践活动课中测量路灯的高度如图,在处测得路灯顶端的仰角为 , 再沿方向前行米到达点处,在处测得路灯顶端的仰角为 , 求路灯顶端到地面的距离点、、在一直线上的长精确到米
参考数据: , , , , ,