湖南省株洲市荷塘区2023年中考数学一模考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
-
1. 下列各数为负数的是( )A、 B、 C、 D、2. 随着人们生活水平的提高,对环境的保护越来越重视,下列垃圾分类标识的图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 据报道:芯片被誉为现代工业的掌上明珠,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到28nm.已知 , 则28nm用科学记数法表示是( )A、 B、 C、 D、5. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )A、24 B、18 C、16 D、66. 不等式的解集在数轴上表示为( )A、
3. 下列计算正确的是( )A、 B、 C、 D、4. 据报道:芯片被誉为现代工业的掌上明珠,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到28nm.已知 , 则28nm用科学记数法表示是( )A、 B、 C、 D、5. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )A、24 B、18 C、16 D、66. 不等式的解集在数轴上表示为( )A、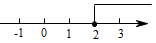 B、
B、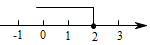 C、
C、 D、
D、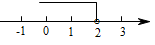 7. 为了解学生课外阅读情况,某校随机抽取了一个班的50名学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是( )
7. 为了解学生课外阅读情况,某校随机抽取了一个班的50名学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是( )读书时间
6小时及以下
7小时
8小时
9小时
10小时及以上
学生人数
5
12
10
13
10
A、10,9 B、10,13 C、8,13 D、8,98. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )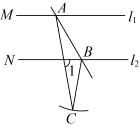 A、 B、 C、 D、9. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )
A、 B、 C、 D、9. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )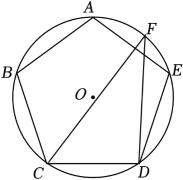 A、38° B、42° C、48° D、58°10. 如图,抛物线的对称轴为 , 与x轴的一个交点在和之间,其部分图象如图所示,则下列结论:
A、38° B、42° C、48° D、58°10. 如图,抛物线的对称轴为 , 与x轴的一个交点在和之间,其部分图象如图所示,则下列结论: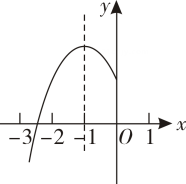
① ;
②;③点、、是该抛物线上的点,则;
④ ;
⑤(t为任意实数).
其中正确结论的个数是( )
A、2 B、3 C、4 D、5二、填空题(本题共8小题,每小题4分,共32分)
-
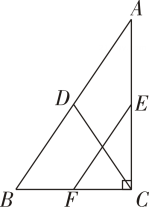
11. 若分式 有意义,则 的取值范围是.12. 写出一个比大且比4小的无理数 .13. 因式分解: .14. 某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这m+n个数据的平均数等于。15. 如图,在中, , 点D , E , F分别为AB , AC , BC的中点,若 , 则CD的长为 .
 16. 如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上, , 反比例函数的图象经过点B,若阴影部分面积为4,则k的值为 .
16. 如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上, , 反比例函数的图象经过点B,若阴影部分面积为4,则k的值为 .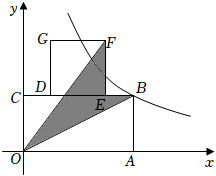 17. 如图,正方形ABCD的边长为3,点E , F分别在BC , CD上,且 , 连接AE , BF交于点P , 连接PD , 则的值为 .
17. 如图,正方形ABCD的边长为3,点E , F分别在BC , CD上,且 , 连接AE , BF交于点P , 连接PD , 则的值为 . 18. 新定义:由边长为1的小正方形构成的网格图形中,每个小正方形的顶点称为格点.如图,已知在5×5的网格图形中,的顶点A、B、C都在格点上,则; .
18. 新定义:由边长为1的小正方形构成的网格图形中,每个小正方形的顶点称为格点.如图,已知在5×5的网格图形中,的顶点A、B、C都在格点上,则; .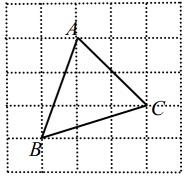
三、解答题(本大题共8小题,共78分)
-
19. 计算:(1) .20. 先化简,再求值: , 其中 .21. 如图,点E是正方形ABCD的边BC上的动点, , 且 , .
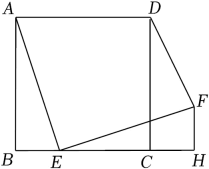 (1)、求证:;(2)、若 , , 求DF的长.22. 如图所示,某大楼的顶部竖有一块广告牌CD , 点C、D、E在同一直线上,且 , 小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为 , 且 . 沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 , 米,米.(测角器的高度忽略不计)
(1)、求证:;(2)、若 , , 求DF的长.22. 如图所示,某大楼的顶部竖有一块广告牌CD , 点C、D、E在同一直线上,且 , 小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为 , 且 . 沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 , 米,米.(测角器的高度忽略不计)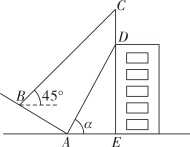 (1)、求点B距水平地面AE的高度;(2)、若市政规定广告牌的高度不得大于9米,请问该公司的广告牌是否符合要求,并说明理由.23. 2023年3月22日是第三十一届“世界水日”,某校举行了水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
(1)、求点B距水平地面AE的高度;(2)、若市政规定广告牌的高度不得大于9米,请问该公司的广告牌是否符合要求,并说明理由.23. 2023年3月22日是第三十一届“世界水日”,某校举行了水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.成绩x/分
频数
频率
15
0.1
a
0.2
60
b
45
c
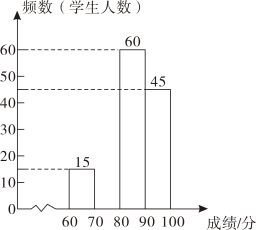 (1)、表中 , , ;(2)、请补全频数分布直方图;(3)、若该校共有3600名学生,估计在知识竞赛中取得90分以上的学生大约有多少名?24. 如图,正比例函数与反比例函数的图象交于点 , 点P是反比例函数图象上的一动点.过点P作轴,垂足为H , 交直线于点G .
(1)、表中 , , ;(2)、请补全频数分布直方图;(3)、若该校共有3600名学生,估计在知识竞赛中取得90分以上的学生大约有多少名?24. 如图,正比例函数与反比例函数的图象交于点 , 点P是反比例函数图象上的一动点.过点P作轴,垂足为H , 交直线于点G .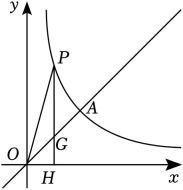 (1)、求k与m的值;(2)、若的面积是2,求此时点P的坐标.25. 已知,如图,AB是的直径,点C为上一点,于点F , 交于点E , AE与BC交于点H , 点D为OE的延长线上一点,且 .
(1)、求k与m的值;(2)、若的面积是2,求此时点P的坐标.25. 已知,如图,AB是的直径,点C为上一点,于点F , 交于点E , AE与BC交于点H , 点D为OE的延长线上一点,且 .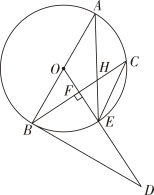 (1)、求证:BD是的切线;(2)、连接BE , 求证:;(3)、若的半径为10, , 求BH的长.26. 如图1,抛物线经过 , 两点,与y轴相交于点C , 连接BC , 点P为线段BC上方抛物线上一动点(不含点B、C),过点P作x轴的垂线l , 交BC于点G , 交x轴于点E .
(1)、求证:BD是的切线;(2)、连接BE , 求证:;(3)、若的半径为10, , 求BH的长.26. 如图1,抛物线经过 , 两点,与y轴相交于点C , 连接BC , 点P为线段BC上方抛物线上一动点(不含点B、C),过点P作x轴的垂线l , 交BC于点G , 交x轴于点E .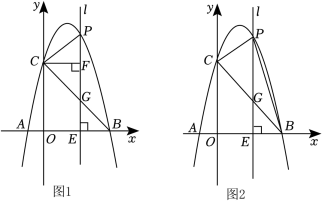 (1)、求抛物线的表达式.(2)、过点C作直线l , F为垂足,当点P运动到何处时,以P , C , F为顶点的三角形与相似?并求出此时点P的坐标.(3)、如图2,连接PC , PB , 请问的面积S能否取得最大值?若能,请求出最大面积S , 并求出此时点P的坐标;若不能,请说明理由.
(1)、求抛物线的表达式.(2)、过点C作直线l , F为垂足,当点P运动到何处时,以P , C , F为顶点的三角形与相似?并求出此时点P的坐标.(3)、如图2,连接PC , PB , 请问的面积S能否取得最大值?若能,请求出最大面积S , 并求出此时点P的坐标;若不能,请说明理由.